Uma das possibilidades que mais me interessam a partir dos Ciclos Intervalares é a construção de sequências de simultaneidades (ou de escalas, de modos, de acordes, enfim, de materiais musicais mais ou menos constantes) sobre eles. Imagine, por exemplo, construir, sobre o ciclo de quartas aumentadas, tríades maiores, resultando na repetição cíclica de C e Gb. Imagine, agora que preenchamos a distância com outros acordes e talvez tenhamos algo como C6 | Abm7 Db7 | Gb6 | Abm7 G7.
Neste texto, discutirei as estruturas resultantes dessas possibilidades – que chamarei de sistemas multi-tônicas e progressões axiais – como uma interferência entre ciclos intervalares e classes de conjunto. Começarei definindo os dois conceitos e o exemplo paradigmático de Giant Steps. Em seguida, farei uma brevíssima revisão das noções de ciclos intervalares e de classes de conjunto de cardinalidade 3 (tricordes). Na discussão propriamente dita, introduzirei uma versão bastante simplificada da Teoria Especial de Harmonia de Joseph Schillinger, diferenciando harmonia diatônica, diatônica-simétrica e simétrica e debatendo ambas como interferências estruturas de fundamentais e qualidades de acordes (classes de conjuntos). Por fim, discutirei algumas comparações (modos de transposição limitada, padrões melódicos e escalas simétricas) e proporei alguns modos para aplicar toda essa discussão.
Progressões Axiais e Sistemas Multi-tônica
Os dois conceitos são relacionados – e até mesmo me parecem ser só olhares diferentes sobre uma mesma ideia – mas é importante defini-los de partida. Keith Waters define a noção de progressão (ou movimento) axial como “Movimento harmônico, melódico ou do baixo sequencial por um único intervalo (2ª menor, 2ª maior, 3ª menor, 3ª maior, etc.)”, que pode ser “elaborado por outras alturas” e geralmente “preservam o mesmo tipo de acorde (como M7) ao se moverem pelo eixo” (2019, p. xix). A sequência Cmaj7 Amaj7 F#maj7 Ebmaj7, por exemplo, é uma progressão axial sobre o eixo de 3 semitons descendente, ou, para usar a linguagem de “O que é um ciclo intervalar?”, sobre o ciclo de 9 semitons. De modo semelhante, progressões parciais (como Cmaj7 Amaj7 F#maj7) são progressões axiais parciais ou truncadas: elas seguem o eixo, mas não o completam.
Um sistema multi tônicas, como definido por Steve Rochinski (2022), é uma técnica de modulação que distribui centros tonais por divisões simétricas da oitava, ou seja, sobre ciclos intervalares. Rochinski também aponta o uso de sistemas multi-tônica incompletos. Num contexto tonal, sistemas multi-tônicas geralmente demandam que os acordes que definirão as tônicas sejam tonicizados por cadências. No exemplo do início do texto (C6 | Abm7 Db7 | Gb6 | Abm7 G7), temos um sistema multitônica construído sobre c6 (seis semitons dividindo uma oitava em 2 partes iguais) centrados em C (0) e Gb (6) e Abm7 Db7 e Abm7 G7 funcionam como ii-V de Gb6 e C6 para tonicizá-los. Tradicionalmente, sistemas multitônicas mantém a mesma qualidade de acorde para cada uma das tônicas e os reservam aos acordes tônicos – ou seja, no nosso exemplo, as qualidades de acorde maior com sexta não devem aparecer nas outras partes da progressão. Rochinski entende que um sistema multi-tônica é diferente de uma progressão de estrutura constante, como seria simplesmente a alternação entre C6 e Gb6 (mesma qualidade de acorde – e preferencialmente mesmo voicing) e deve ter embelezamentos, prolongamentos e cadências.
Ainda que, em ambos os casos, o uso tradicional seja destacar o movimento cíclico e, em certo sentido, paralelo entre as tônicas da estrutura, gosto de pensá-las modalmente também. Isso é: não realizá-la necessariamente como C6 para Gb6, mas de C jônio (024579B) para Gb jônio (68AB135) que podem ser substituídos por seus modos. Talvez C jônio para Ab dórico para F lídio para Gb jônio e assim por diante, alternando entre as duas transposições de 7-35 mas em rotações diferentes.
Giant Steps
Uma progressão de acordes tradicionalmente tonal – viiº-iii-vi-ii-V-I – e suas simplificações e variações, como as progressões utilizadas em I Got Rhythm (VI-ii-V-I e III-VI-II-V), são um caso pouco interessante de algo que pode ser lido como uma progressão axial ou sistema multi-tônicas parcial construída sobre o ciclo de quartas ascendentes (C5). Ainda que seja possível construir progressões axiais e sistemas multi-tônica sobre os ciclos de cinco e sete semitons (quartas e quintas justas), ou explicar, à força, progressões tonais a partir desta lógica, os casos mais interessantes residem nas progressões que resultam efetivamente em sistemas multi-tônica exteriores às formulas tonais.
O caso mais notório – e o caso paradigmático apontado tanto por Rochinski quanto Waters – é a progressão de Giant Steps e as rearmonizações que Coltrane realizou sobre diversos standards usando progressões axiais e sistemas multi-tônica. Em Giant Steps, Coltrane circula rapidamente por três campos harmônicos maiores: B, G e Eb, tonicizados com ii-V7 ou V7. Na imagem abaixo, marquei com cores diferentes as regiões da música relativas a cada uma das multi-tônicas, inclui as cadências (ii-V7) que estabelecem cada tônica como parte da tonalidade resultante.
Coltrane ascende e descende pelas tônicas e é difícil, pro ouvinte ou pra um improvisador, determinar qual das três notas seria a tônica da música. Difícil, mas também desnecessário: a ideia é justamente ocupar as três tônicas, circular entre elas para produzir um tonalismo cromático e metaestável.
Breve Revisão: ciclos intervalares e classes de conjunto de cardinalidade 3
Um ciclo intervalar é uma estrutura musical gerada pela repetição sucessiva de um intervalo fixo dentro de um sistema de notas. Esse ciclo é construído ao somar iterativamente um intervalo a uma nota inicial até que se retorne à mesma nota em uma oitava superior. Por exemplo, a escala cromática pode ser vista como um ciclo intervalar de segundas menores (semitons), em que cada nota é gerada somando um semitom à anterior (C, C#, D, D# etc.). Alguns intervalos geram ciclos intervalares que se repetem dentro de uma oitava (1, 2, 3, 4 e 6 semitons) ou maiores que uma oitava (5, 7, 8, 9, 10 e 11). Neste texto, vou me referir aos ciclos somente dentro de uma oitava, de modo que, por exemplo, o ciclo de 8 semitons (0 8 4 0) será simplesmente um ciclo de 4 semitons (0 4 8 0) descendente e agrupá-los por classe de intervalo e em quantas partes dividem a oitava.
| Ciclo | Divisão | Equivalente | Notas geradas |
| c1 | 12 partes | c11 | 0123456789AB0 |
| c2 | 6 partes | c10 | 02468A0 |
| c3 | 4 partes | c9 | 03690 |
| c4 | 3 partes | c8 | 0480 |
| c5 | 12 partes | c7 | 05A3816B49270 |
| c6 | 2 partes | – | 060 |
Aqui a diferença entre progressão axial e sistema multi-tônicas tem alguma relevância. Em primeiro lugar, as progressões axiais sobre C5, C7, C11 e C1 são obviamente diferentes, mas um sistema multi-tônica construído sobre eles não é. Nos três casos, geram-se doze tônicas contendo toda a escala cromática em alguns casos contendo os mesmos acordes, entretanto, dependendo do processo, em especial dos coeficientes de recorrência, geramos sistemas multi-tônicas com qualidades de acorde diferentes entre eles. O mesmo vale para c9 e c3, por exemplo. Em segundo lugar, a direção de uma progressão axial sobre, por exemplo c4, é diferente da progressão sobre c8 (c4 descendente), enquanto num sistema multi-tônicas a ordem das tônicas é mais determinada pelo sentido da progressão (positiva ou negativa) e pelo movimento determinado pelo compositor entre as tônicas do que pela estrutura do ciclo gerador. Uma discussão mais aprofundada pode ser encontrada no texto O que é um ciclo intervalar?.
Classes de conjunto são, por outro lado, abstrações de coleções de três classes de notas, para repetir a definição tradicional: são como que pequenos motivos dos quais a maior parte das características foram abstraídas até chegar no conteúdo de classes de notas e abstraídas mais uma vez para chegar a uma estrutura intervalar básica. Por exemplo, uma passagem que contém as notas da escala maior de fá, pode ser abstraída até chegar somente nas classes de nota – independente do registro, do ritmo, da ordem, da repetição de notas: 579A024 (ou F, G, A, Bb, C, D e E). Ela pode ser abstraída, por simplificação e rotação, de modo a ser organizada como uma estrutura intervalar +1 +2 +2 +1 +2 +2, representada, a partir de 0 como 0,1,3,5,6,8,T. Essa classe de conjunto, chamada 7-35 representa, abstratamente, todas as transposições de todos os modos da escala diatônica. O processo para chegar nessa abstração foi descrito no texto Que acorde é esse?.
Algumas classes de conjunto são inversíveis e notamos as duas inversões como A e B, T e I, a depender do contexto. Os conjuntos concretos existem sempre em alguma transposição, a escala maior de fá, por exemplo, é 7-35 T4 (4579A02) – transposta 4 semitons – e o acorde de E maior é 3-11 I4.
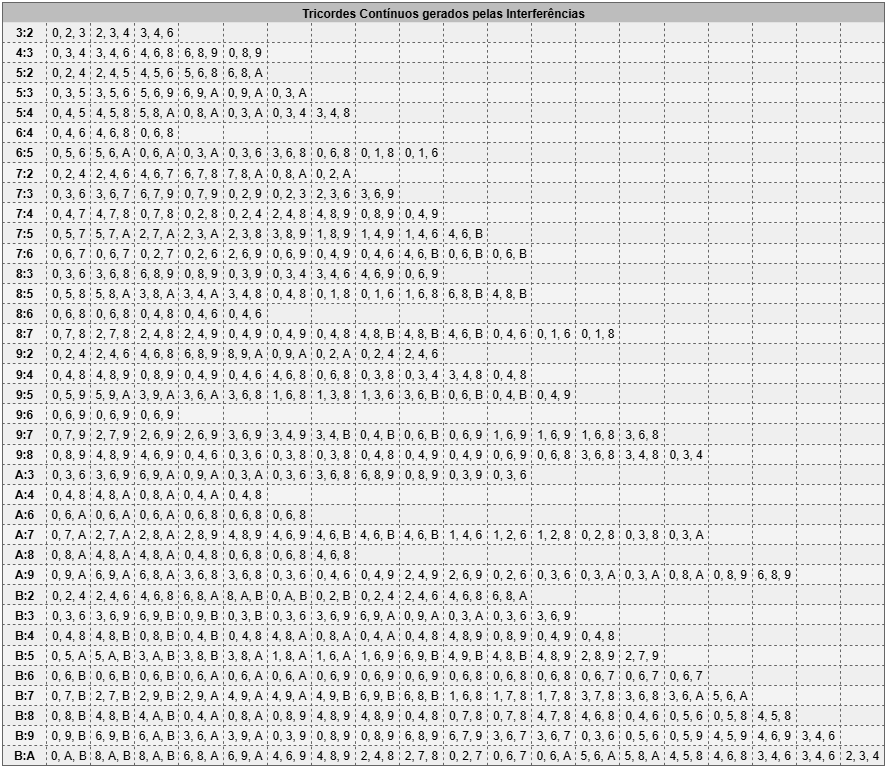
Por simplicidade, pela quantidade manejável e pela possibilidade de compor estruturas maiores com facilidade, tenho optado por trabalhar com conjuntos de cardinalidade 3 ou tricordes, isso é: conjuntos de três classes de notas. Na tabela abaixo, retirada do texto Que acorde é esse?, listo todas as classes de conjunto de cardinalidade 3 possíveis no sistema de 12 tons e uma proposta de cifragem.
| Conteúdo | CC | Tipo | Cifra | Voicing | Intervalo de Produção |
|---|---|---|---|---|---|
| 012 | 3-1 | E | Db^7M(b9) | 102 | Segundas |
| 013 | 3-2A | E | Db^7M(9) | 103 | Segundas |
| 023 | 3-2B | E | D^7(b9) | 203 | Segundas |
| 014 | 3-3A | C | C#^m7M | 140 | Mistos (semitom) |
| 034 | 3-3B | D | E^7M(#5) | 403 | Mistos (semitom) |
| 015 | 3-4A | C | Db7M(¬5) | 150 | Mistos (semitom) |
| 045 | 3-4B | D | F^7M(5) | 504 | Mistos (semitom) |
| 016 | 3-5A | B | DbQT | 160 | Quartas |
| 056 | 3-5B | B | F#TQ | 605 | Quartas |
| 024 | 3-6 | E | D^7(9) | 204 | Segundas |
| 025 | 3-7A | C | D^m7 | 250 | Mistos (pentatônicos) |
| 035 | 3-7B | D | F^7(5) | 503 | Mistos (pentatônicos) |
| 026 | 3-8A | C | Dit ou D7(¬5) | 260 | Mistos (tons inteiros) |
| 046 | 3-8B | D | F#^7(b5) | 604 | Mistos (tons inteiros) |
| 027 | 3-9 | B | DQ3 | 270 | Quartas |
| 036 | 3-10 | A | Cdim | 036 | Terças |
| 037 | 3-11A | A | Cm | 037 | Terças |
| 047 | 3-11B | A | C | 047 | Terças |
| 048 | 3-12 | A | Caug ou C(#5) | 048 | Terças |
Obviamente, esses tricordes podem ser combinados, transpostos, realizados em diferentes rotações e aberturas… Caso tenha interesse, na seção “Complementos”, disponibilizei a cifragem de cada transposição destes conjuntos e um dicionário de formas acorde para os tricordes.
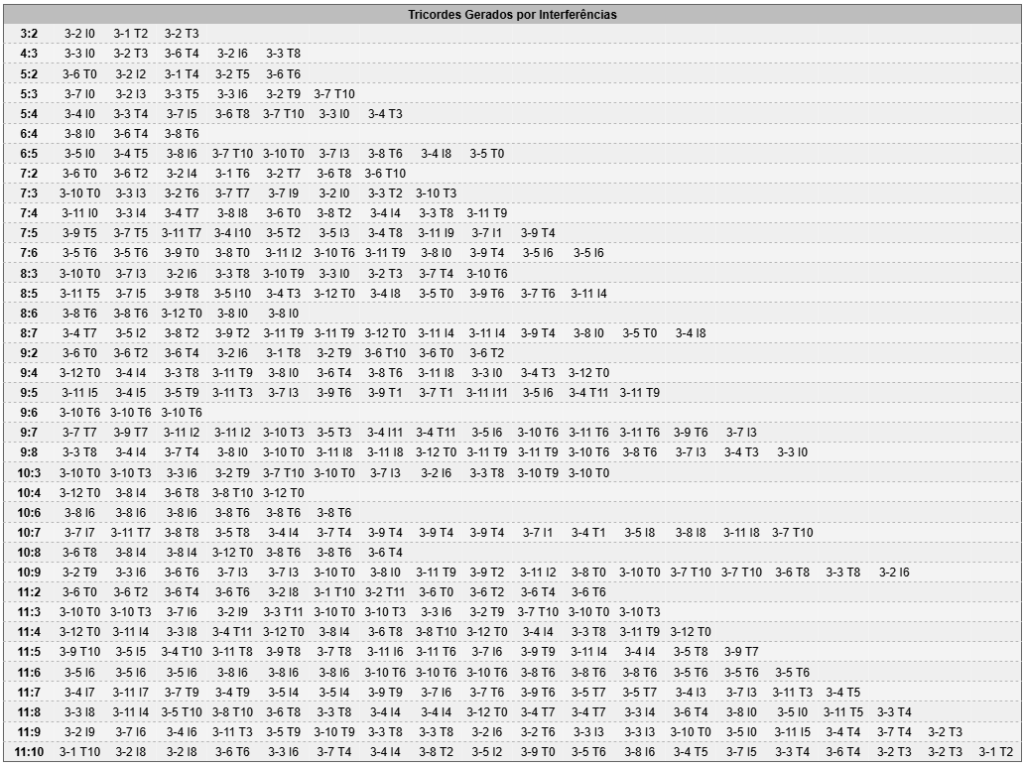
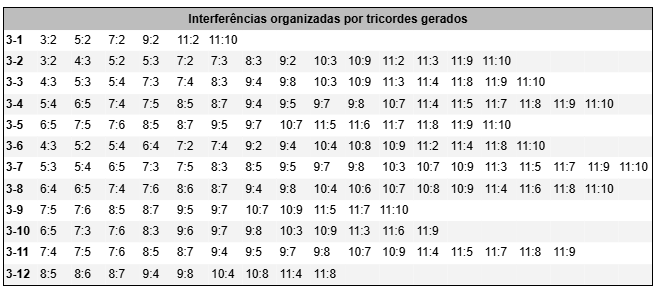
Tricordes e ciclos ainda são materiais muito elementares: “o que eu faço com isso?” me parece a pergunta mais óbvia. Qualquer coisa, eu diria, mas também sei o quão paralisante é a página em branco e listas imensas de possibilidades. Num texto anterior (Tricordes como Interferência entre Ciclos Intervalares), tentei propor uma lógica de selecionar e organizar os tricordes a partir da interferência entre dois ciclos. O resultado é interessante: sequências de tricordes diferentes, mas internamente coerente, dotadas de uma direcionalidade intrínseca e de uma lógica de condução de vozes derivada dos mesmos ciclos que os geram, mas ainda são progressões prontas, excessivamente orgânicas talvez. A teoria de Schillinger, onde ciclos interferem com qualidades de acordes, oferece uma opção mais aberta.
Teoria Especial da Harmonia de Joseph Schillinger
A teoria especial de harmonia é o quinto livro do Sistema Schillinger de composição musical e usa conceitos introduzidos nos livros anteriores, além da linguagem matemática peculiar de Joseph Schillinger. Esta seção, por isso, não é uma introdução ou análise, mas uma pilhagem da teoria.
O livro cobre diversos assuntos, mas vou focar nos primeiros tópicos discutidos, a saber: a harmonia diatônica, simétrica e diatônica-simétrica, que são três casos de combinação de dois mecanismos de seleção. Por um lado, temos a seleção da progressão de fundamentais dos acordes, que pode ser definida por uma escala (e um ciclo tonal interno à escala) ou por um ciclo intervalar (uma divisão simétrica da oitava). No primeiro caso, temos harmonia diatônica e diatônica simétrica, no segundo, simétrica. Por outro lado, temos a seleção das estruturas (ou qualidade) dos acordes, que pode ser feita a partir da escala (na harmonia diatônica) ou pré-selecionados (na harmonia simétrica e diatônica-simétrica).
| Harmonia | Fundamentais | Acordes |
| Diatônica | Ciclos tonais internos à escala | Retirados da escala |
| Diatônica-Simétrica | Ciclos tonais internos à escala | Pré-selecionados |
| Simétrica | Ciclos intervalares e divisões simétricas da oitava | Pré-selecionados |
Um terceiro mecanismo, que não discutirei aqui, diz respeito à condução de vozes e à rotação dos acordes (voicing) sobre as fundamentais. Mas vale dizer que a introdução de acordes diversos à harmonia tonal, colocam problemas sobre condução de vozes e levantam o debate sobre a existência de contraponto pós-tonal. Como conduzir parcimoniosamente, por exemplo, entre 3-1 T0 e 3-7 T2?
A prioridade deste texto é a harmonia simétrica, mas passarei pela harmonia diatônica e diatônica-simétrica porque elas possuem práticas em comum e uma progressão de complexidade.
Harmonia diatônica
A harmonia diatônica, como disse, retira o movimento das fundamentais e os acordes de uma mesma escala de referência. Schillinger, na teoria especial de harmonia, foca na escala diatônica, mas parece-me que funcionaria do mesmo modo com outras escalas e com os acordes “diatônicos” a essa escala. Nesta seção, usarei como exemplo a escala diatônica (024579B) e o Lídio 7#2b6 (034678A).
Na sua própria definição a “Teoria especial de harmonia é restrita a E1 do primeiro grupo de escalas, que contém todos os nomes musicais (c, d, e, f, g, a, ) e sem repetição”. O primeiro grupo de escalas de Schillinger, são as escalas de 1 a 11 classes de notas, restritas a uma oitava. Neste capítulo, ele se limita às escalas de sete notas em primeira expansão (E1). As expansões das escalas são ordenamentos da escala de modo a formar uma estrutura uniforme. A forma original da escala (E0) é a escala ordenada em graus conjuntos. E1 é a escala ordenada em terças – do mesmo modo como na teoria acorde escala. E2 é a escala construída “em quartas” e assim por diante. Na imagem abaixo, as duas escalas que usaremos aparecem em E0, E1, e E2.


As escalas, em Schillinger, são conjuntos ordenados e os acordes são os conjuntos discretos gerados pelas expansões. Abaixo, os acordes da primeira expansão das duas escalas construídos sobre C no que Schillinger chama de forma positiva. Não discutirei a forma negativa.

No caso da escala diatônica, isso seja só um jeito desnecessariamente complicado de dizer: acordes de qualquer cardinalidade construídos em terças sobre a escala. No caso de escalas sintéticas e exóticas, onde a noção de “terça” genérica pode variar de 2 a 5 semitons, parece-me uma forma mais natural de entender as estruturas geradas. O mesmo poderia ser feito com as outras expansões. No exemplo abaixo, os acordes gerados sobre a segunda expansão das duas escalas sobre C.

A progressão das fundamentais dos acordes acontece sobre ciclos tonais que Schillinger nomeia: ciclo das terças, ciclos de quintas e ciclo de sétimas que ele constrói descendentemente sobre os intervalos de terça, quinta e sétima genéricos da escala. Vale notar, que Schillinger distingue entre a forma harmônica (HS) e a forma melódica (MS) da escala. HS é construído descendentemente sobre a primeira expansão de MS. Na imagem abaixo os três ciclos são nomeados pela expansão da escala harmônica e pelo tipo de ciclo tonal (Cn). As notas ligadas representam os movimentos cadenciais de cada ciclo, entendidas como o movimento de ida e volta entre acordes adjacentes no ciclo. O primeiro são as cadências de abertura (C para F no ciclo de quintas) e os últimos são as cadências de fechamento (G para C no ciclo de quintas).

Uma progressão por qualquer um dos ciclos tonais produz uma sequência contendo os sete acordes da escala. Progressões mais interessantes podem ser geradas combinando ciclos para gerar progressões binomiais (dois ciclos) ou trinomiais (três ciclos). Progressões binomiais envolvem o movimento intercalado entre dois ciclos, por exemplo: no binômio C3+C5, começando em C, movemos para A por C3, de A para D por C5, de D para B por C3 e assim por diante. Na imagem abaixo, notei as fundamentais da progressão binomial C3 + C5.

Nas progressões trinomiais, os três ciclos são combinados intercaladamente. No caso, de C7 + C3 + C5, partindo de C para D por C7, para B por C3, para E por C5, para F por C7 e assim sucessivamente até retornar a C. Na imagem abaixo, o mesmo trinômio é construído sobre o Lídio 7#2b6 e em seguida harmonizado com tricordes retirados de E1 desta escala. Observe que as fundamentais dos acordes são notadas com a cabeça vazada e o ordenamento e a sequência dos acordes priorizou um movimento ascendente com condução parcimoniosa de vozes.


Uma terceira possibilidade é a criação de progressões polinomiais, onde cada ciclo é repetido certo número de vezes. Por exemplo, na escala diatônica, o polinômio 2C3 + C5, partindo de C para A e depois F por C3 e de F para B por C5. Os números atribuídos a cada ciclo é chamado por Schillinger de Coeficiente de Recorrência.

Os polinômios podem ficar tão complexos quanto o compositor quiser e podem ser usados em combinação com outras técnicas, como a sincronização binária da teoria do ritmo. A sincronização de 3 e 2 (3:2), por exemplo, gera o seguinte padrão: 2 1 1 2.

Podemos utilizá-lo fazendo interferir sobre C7 + C5 para gerar 2C7 + 1C5 + 1C7 + 2C5. Observe que, para completar a progressão, é preciso múltiplas iterações do polinômio até retornar ao mesmo C (notadas com notas ligadas).

Os diferentes tipos de continuidade (progressões monomiais, binomiais, trinomiais, polinomiais e mais complexas) geram estilos harmônicos que o compositor pode usar em contexto diatônico. Depois de selecionada a progressão das fundamentais, resta escolher o tipo de estrutura dos acordes a serem construídos sobre as fundamentais. No caso de Schillinger, essas estruturas são as tríades da primeira expansão da escala diatônica e mais acima exemplifique construíndo uma progressão sobre as tríades da primeira expansão do Lídio 7#2b6. Outras estruturas poderiam ser usadas, mesmo no caso da escala diatônica. Os tricordes 3-2, 3-4, 3-5, 3-6, 3-7, 3-8, 3-9, 3-10 e 3-11 são, por exemplo, subconjuntos da escala diatônica e poderiam ser utilizados. Obviamente nem todos os tricordes podem ser construídos sobre os graus e seria preciso – se quisermos manter a consistência do sistema – um jeito de identificar a expansão que resultaria em cada um deles. Uma maneira mais fácil seria deslizar as vozes dos tricordes pela escala. Na imagem abaixo, deslizo sobre C3+C5 o tricorde 3-6 (024) – construído como tônica, terça e nona genéricas da escala – resultando em uma progressão que varia entre 3-6, 3-2A e 3-2B. Não me preocupei com condução parcimoniosa de vozes, para facilitar a identificação dos tricordes.

De qualquer modo, na harmonia diatônica, mesmo expandindo as estruturas de acorde aceitáveis, ainda estamos limitados aos subconjuntos da escala diatônica ou de referência escolhida. As harmonias simétricas nos dão outras possibilidades harmônicas, politonais, cromáticas etc.
Harmonia diatônica-simétrica
A harmonia diatônica-simétrica mantém o movimento das fundamentais pelos ciclos tonais internos à escala de referência – seja diatônica, seja sintética – mas usa um mecanismo de seleção dos acordes diferentes. Nela, as estruturas dos acordes são pré-selecionadas e usadas cromaticamente. Isso quer dizer que, se selecionarmos, por exemplo, a tríade menor e a escala diatônica, todos os acordes serão tríades menores, independentemente da fundamental. No exemplo abaixo, a tríade menor é construída sobre a progressão C3 + C5.

Mesmo com uma única estrutura e uma progressão sobre ciclos tonais diatônicos, o resultado é uma saturação cromática: somente a classe de notas 1 (C#) não está presente. Entretanto, é possível construir progressões com mais de uma estrutura. Com múltiplas estruturas, começamos a gerar progressões ainda maiores. Se escolhermos, por exemplo, 3-7A e 3-7B sobre C3 é preciso passar duas vezes pelo ciclo antes de a progressão se completar, i.e. retornar à mesma estrutura no mesmo momento do ciclo. Abaixo realizei o ciclo intercalando 3-7A e 3-7B, no primeiro sistema em um aversão literal, na segunda, em um voicing diferente, buscando melhor condução de vozes.


Observe que cada estrutura, aparece uma veze sobre a mesma fundamental – de modo que cada fundamental aparece sob duas estruturas diferentes em momentos diferentes da progressão. Mesmo com tríades mais tonais, é possível gerar progressões bastante cromáticas. No exemplo abaixo, 3-11A e 3-11B, respectivamente o tricorde menor e o tricorde maior, são construídos sobre o ciclo C3, numa primeira realização literal e depois com melhor condução de vozes.
Na harmonia diatônica-simétrica, também é possível construir progressões trinomiais, que não exemplificarei, e polinomiais usando coeficientes de recorrência diversos para cada estrutura, além de combinações de diferentes ciclos tonais com coeficientes diferentes. As resultantes de combinar ambos os processos (progressão polinomial sob estrutura polinomial) tornam-se rapidamente muito grandes e complexas. Utilizemos a estrutura polinomial 2x + 1y para a progressão das fundamentais e para os tricordes. Para as fundamentais x=C3 e y=C7. Para as estruturas x= 3-9 (027) e y= 3-5B (056), construídos, respectivame nte como Q3 (tricorde quartal) e TQ (tricorde de trítono e sétima maior).

No exemplo acima, como utilizamos o mesmo binômio, apesar de longa, o ciclo das fundamentais só precisou repetir-se uma vez antes de se completar. Mas utilizando coeficientes de recorrência diferentes para a progressão das fundamentais e para a recorrências das estruturas, múltiplas voltas serão necessárias.
Um detalhe interessante da harmonia diatônica-simétrica é a produção, nas vozes dos tricordes, de um tipo de politonalismo ou polimodalismo ou o que se queira chamar a simultaneidade de mais de uma transposição de uma escala ou de escalas diferentes nas vozes. No caso de uma progressão simples – i.e. uma progressão sobre um ciclo tonal com uma estrutura – produzimos escalas paralelas distando a estrutura do acorde. Por exemplo: 027 sobre qualquer ciclo, se todas os acordes estiverem na mesma posição, por exemplo, como Csus2, Dsus2, Esus2 e etc. Temos a escala maior de C, D e G soando simultaneamente.
A harmonia diatônica-simétrica, pela referência escalar, mesmo polimodal, nos mantém ainda, em certo sentido, dentro de um cromatismo diatônico à escala de referência, com suas implicações de polarização e de hierarquias tonais. Quando partimos para a harmonia simétrica pura, isso é substituído – finalmente – por um sistema multi-tônicas.
Harmonia simétrica
Na harmonia simétrica a seleção das fundamentais não está centrada em nenhuma escala, mas em ciclos intervalares propriamente ditos, entendidos aqui como divisões simétricas da oitava. Tanto as estruturas quanto a progressão das fundamentais é pré-selecionada independentemente da escala. É importante que, para ser harmonia simétrica, as estruturas selecionadas não podem ser subconjuntos da classe resultante do ciclo empregado. Por exemplo, se escolhermos 3-8A (026) como a estrutura e o ciclo de dois semitons (que resulta na escala de tons inteiros) como progressão das fundamentais, não geramos uma harmonia simétrica propriamente dita, já que as estruturas são subconjuntos da escala de tons inteiros. Neste caso, teríamos uma harmonia diatônica – ainda que não sobre a escala diatônica, mas diatônica à escala pré-selecionada.

O primeiro caso de harmonia simétrica que Schillinger cita, entretanto, não é construído sobre um ciclo que divide a oitava em partes, mas na própria oitava – ou uníssono – o ciclo de 0 semitons. Neste caso, um número de estruturas pré-selecionadas é tocado sobre a mesma fundamental. Este tipo de progressão, diz Schillinger, “pode ser uma forma independente de continuidade harmônica ou uma parte de outras formas simétricas” (1946, p. 391). Como continuidade harmônica independente, podemos pensar este tipo de harmonia como uma progressão sobre um baixo ou outro tipo de pedal.


O ciclo zero, como disse, não é exatamente um ciclo, mas a oitava: ele divide um espaço de notas idealmente infinito em oitavas e – em função da equivalência de oitava – divide a oitava em 1 tônica. As outras divisões da oitava são geradas pelos ciclos intervalares. Há cinco sistemas multi-tônicas:
| Sistema | Tônicas (em inteiros) | Ciclos correspondentes |
| Duas tônicas | 0-6-0 | ic6 |
| Três tônicas | 0-4-8-0 | ic4 e ic8 |
| Quatro tônicas | 0-3-6-9-0 | ic3 e ic9 |
| Seis tônicas | 0-2-4-6-8-A | ic2 e ic10 |
| Doze tônicas | 0-1-2-3-4-5-6-7-8-9-A-B | ic1, ic11, ic5 e ic7 |
Rochinski, embasado, creio, na leitura berkleeana do sistema Schillinger, adiciona dois pontos importantes: primeiramente, as tônicas podem representar centros tonais (de um modo, ou escala) ou fundamentais de acordes. Em segundo lugar, somente os sistemas de 3 e 4 tônicas são fundamentais, os outros são derivados. O sistema de 2 tônicas (0-6-0) é o sistema de 4 (0-3-6-9-0) tônicas reduzido; o sistema de 6 tônicas (0-2-4-8-A-0) é uma combinação de dois sistemas de 3 tônicas (0-4-8-0) separados por 2 semitons. Os sistemas de 12 tônicas são raramente usados enquanto sistemas multi-tônica e podem ser usados como progressões axiais parciais.
Duas observações adicionais são importantes. Primeiramente, é possível usar múltiplas estruturas de acorde, construir progressões com coeficientes de recorrência para cada estrutura e mesmo para os ciclos. Em segundo lugar, as progressões geradas devem ser encaradas como esqueletos ou fundo, não necessariamente como progressões literais. Isso quer dizer: o compositor deve se sentir convidado a adicionar notas e acordes de passagem, desenvolver as progressões com extensões, embelezamentos, substituições e o que mais achar apropriado. Na discussão a seguir, vou me limitar ao esqueleto, geralmente com só um tipo de estrutura.
Sistema de duas tônicas
O sistema de duas tônicas é construído sobre o ciclo de seis semitons. Considerando a prática de condução de vozes de Schillinger, o sistema de duas tônicas forma o que ele chama de sistema contínuo. Isso é, se rotacionarmos, a cada tônica, o acorde usado, o sistema leva mais de uma interação para se completar – ou seja, retornar ao mesmo acorde, na mesma rotação, na mesma tônica. No exemplo abaixo, utilizo, como Schillinger, o acorde maior como estrutura, mas mudando a rotação tônica gerando um padrão ascendente em cada voz.

Com a tônica no baixo e o resto do acorde nas vozes superiores é possível ver que a mesma escala é gerada em cada voz: 6-34 (468A01).
Se utilizarmos tricordes mais interessantes, como Q3 (027), problemas de condução de vozes começam a aparecer, mas obtemos harmonias mais exóticas.

Novamente, a mesma escala é produzida em cada voz. Neste caso 6-7 (012678). Sugiro testar conduzir as vozes usando 8-25 (0124678A) para conduzir as vozes que saltam 3 semitons, especificamente usando 4 para conduzir de 2 a 6 e A para conduzir de 8 a 0.
A progressão das tônicas não chega a constituir uma escala da qual podemos extrair tricordes, já que é só uma díade (0-6). Mas é importante observar que tricordes derivados dos ciclos de 3 e 4 semitons, respectivamente 3-10 (036) e 3-12 (048) podem obscurecer o caráter simétrico da harmonia, pois resultam, respectivamente no tetracorde diminuto ou 4-28 (0369) – as fundamentais do sistema de 4 tônicas e o ciclo de três semitons – e na escala de tons inteiros ou 6-35 (02468A) – o sistema de seis tônicas e o ciclo de dois semitons.

Sistema de três tônicas
O sistema de três tônicas é construído sobre o ciclo de quatro semitons (048) ou de oito semitons (084). Os subconjuntos a serem evitados são a terça maior (04) e o tricorde aumentado (048), que é idêntico ao ciclo das fundamentais. Em ambos os casos, o resultado é a escala resultante da progressão das fundamentais, o que configuraria um sistema diatônico. Todos os subconjuntos de 6-35 (02468A) – 3-6 (024), 3-8A (026) e 3-8B (046) e 3-12 (048) – também devem ser evitados, pois resultam nesta escala, da qual as fundamentais do sistema de três tônicas (048) são subconjunto. O resultado seria uma harmonia diatônica, na escala de tons inteiros seguindo um ciclo tonal CT3 (de terças).
Giant steps e seus derivados diretos são baseados neste sistema. No caso de Giant Steps, o acorde de sétima maior (047B) é construído sobre cada uma das tônicas do sistema começando em B (B37) e depois preenchida com ii-V7-I ou V7-I para tonicizar cada um dos acordes resultantes.

Como o sistema tem 3 tônicas, a rotação de conjuntos de cardinalidade 3 – que possuem 3 rotações – a cada tônica gera um sistema fechado, como no exemplo abaixo, com 3-9 (027).

Utilizando duas estruturas de acorde com recorrência 1, ou intercalando entre posição aberta e fechada, três tônicas geram um sistema contínuo de dois ciclos. No exemplo abaixo 3-7A e 3-7B.

Outra possibilidade, utilizando duas ou mais estruturas é tratar cada tônica como c0 até completar os tricordes. No exemplo abaixo, primeiro 3-7A e 3-7B são construídos sobre 0 (c0) e depois sobre 4 e por fim 8. O resultado é um híbrido de um sistema sobre c0 e sobre c4 contendo 6 acordes sobre três tônicas.

Sistema de quatro tônicas
O sistema de quatro tônicas é construído sobre o ciclo intervalar de quatro semitons (0369) ou de nove semitons (0963). O tetracorde diminuto (4-28), que contém as mesmas notas do ciclo, e 3-10, único tricorde subconjunto de 4-28, devem ser evitados.
Parte da progressão de Litha, de Chick Corea, é construída sobre uma combinação de dois sistemas de quatro tônicas, um começando em Dmaj7 e um começando em C#m7. A progressão resulta de intercalar os dois sistemas descendentemente, como no exemplo abaixo – onde as fundamentais de cada sistema estão diferenciadas por registro.

O resultado é interessantíssimo de um ponto de vista modal. Dmaj7 pode ser lido como sugerindo Jônio ou Lídio. O lídio é confirmado por C#m7, mas quando C#m7 – que deve ser lido como frígio para que Dmaj7 seja lídio – move-se para Bmaj7, sugere C# dórico e B jônio. Quando Bmaj7 move-se para Bbm7, sugere que Bmaj7 é lídio e Bbm7 é frígio, para depois ser dórico em relação a Abmaj7 e assim por diante. O resultando é que ambos os acordes são lidos de um modo como ponto de partida e outro como ponto de chegada. A progressão também pode ser pensada como uma progressão diatônica-simétrica sobre a escala octatônica.
O sistema de quatro tônicas resulta em um sistema contínuo com três ciclos quando rotacionamos as vozes de um mesmo tricorde a cada tônica. No exemplo abaixo, 3-5B (056) é construído trocando de rotação a cada fundamental.

Observe que cada voz forma a escala octatônica ou 8-28 (0235689B), que poderia ser usada para facilitar a condução de vozes. Todos os subconjuntos da escala octatônica, excetuando 3-10 – ou seja, 3-2, 3-3, 3-5, 3-7, 3-8 e 3-11 – geram a escala octatônica quando construídos sobre o sistema de quatro tônicas.

Sistema de seis tônicas
O sistema de seis tônicas é construído sobre o ciclo de dois semitons ou de dez semitons que gera a escala de tons inteiros ou 6-35 (02468A). Subconjuntos desta escala (3-6, 3-8 e 3-12) devem ser evitados, uma vez que resultam em harmonia diatônica sobre 6-35. Os subconjuntos recomendados são 3-1, 3-2, 3-3, 3-4, 3-5, 3-7, 3-9, 3-10 e 3-11.
Muhal Richard Abrams utiliza o sistema de seis tônicas sobre acordes menores com sétima na progressão de Roots. Na transcrição e análise de Marc Hannaford, a peça começa com cinco acordes menores construídos sobre o ciclo (02468A) – e observe que ele não segue o ciclo numa progressão linear, mas utiliza as tônicas geradas sobre o sistema. Eventualmente, Abrams muda para a outra transposição do sistema de seis tônicas (13579B) descendo em graus conjuntos e cercando B – a única tônica não utilizada no primeiro sistema, o que Hannaford vê como um completar do ciclo. As progressões seguintes seguem o sistema de 12 tônicas.
É interessante notar a prevalência do acorde menor com sétima ou 4-26, que contém dois intervalos de ci3 (três semitons) e ci5 (cinco semitons), sobre a escala de tons inteiros, que não contém esses intervalos.
Sistema de doze tônicas
O sistema de seis tônicas é construído sobre os ciclos de um, onze, cinco ou sete semitons. Todos os conjuntos de qualquer cardinalidade, no sistema de 12 notas, são subconjuntos destes ciclos, de modo que é impossível recomendar, a partir deles, uma seleção de tricordes. Entretanto, se considerarmos os ciclos geradores – ou da famílias de ci1 (1 e 11 semitons) ou da família de ci5 (5 ou 7 semitons) – podemos evitar: 1) os tricordes discretos gerados pelo ciclo – ou seja: 3-1 (012) para ci1 e 3-9 (027) para ci5. 2) Tricordes com prevalência de ci1 e ci5 – como 3-2 (013) para ci1 e 3-7 (025) para ci5.
Ainda que, para a geração de progressões completas, esses sistemas sejam de pouca utilidade, eles podem gerar resultados interessantes se forem usadas parcialmente, como no exemplo de Abrams acima. Importante nesses casos priorizar a saturação cromática – ou seja preencher o intervalo da progressão com as fundamentais que caracterizem o sistema – evitar obviedades (no caso de ci1) e implicações tonais (no caso de ci5) e evitar que a progressão das fundamentais resulte em outro ciclo.
Outros Sistemas
Se expandirmos nossa seleção básica de notas – aquela que define a escala cromática de doze tons iguais – por outro sistema de seleção de notas – por exemplo, o sistema de 24 quartos de tom – podemos gerar sistemas multi-tônicas diferentes. Em quartos de tons, por exemplo, o ciclo de 3 quartos de tom (1,5 semitons) gera um sistema de oito tônicas.

Se organizarmos este sistema de oito tônicas alterando a rotação a cada tônica, geramos um sistema contínuo com recorrência a cada três ciclos, como no exemplo abaixo. Observe que, pela extensão da progressão, saltei a cada compasso para favorecer a legibilidade.

Digressão: outras estruturas relacionadas
Há outras formas de pensar sistemas multi-tônicas – que acabam resultando em estruturas semelhantes, mas com lógicas de construção e uso diversas. Imagino que hajam tantas quanto compositores, improvisadores e teóricos interessados nelas, mas focarei em três: nos padrões melódicos de Slonimsky, nos modos de transposição limitada de Messiaen e nas escalas simétricas. Essas duas últimas são semelhantes, mas com usos diferentes.
No Thesaurus of Scales and Melodic Patterns, Slonimsky descreve uma enorme quantidade de escalas e padrões melódicos baseados em divisões simétricas de uma quantidade de oitavas – o mesmo que os ciclos intervalares de 1 a 12 semitons. Na tabela abaixo, apresento os nomes propostos por Slonimsky, a quantidade de divisões do número de oitavas gerado pelo ciclo derivado e o sistema multi-tônicas equivalente. A divisão é representada por n/m onde n é o número de oitavas e m é o número de partes. A divisão ⅔, por exemplo, é a divisão de duas oitavas em três partes.
| Intervalo | Nome | Divisão | Sistema |
| ci1 | Semitom | 1/12 | doze tônicas |
| ci2 | Tom | 1/6 | seis tônicas |
| ci3 | Sesquitom | 1/4 | quatro tônicas |
| ci4 | Ditom | 1/3 | três tônicas |
| ci5 | Diatessarão | 5/12 | doze tônicas |
| ci6 | Tritom/Trítono | 1/2 | duas tônicas |
| ci7 | Diapente | 7/12 | doze tônicas |
| ci8 | Quadritom | 2/3 | três tônicas |
| ci9 | Sesquiquadritom | 3/4 | quatro tônicas |
| ci10 | Quinquetom | 5/6 | seis tônicas |
| ci11 | Sesquiquinquetom | 11/12 | doze tônicas |
Essa estrutura básica – idêntica aos ciclos apresentados no texto O que é um ciclo intevalar? – define os tons principais que são ornamentados com notas adicionais. Essa ornamentação é sempre idêntica para cada tom principal. Por exemplo, se estamos construíndo um padrão sobre os tons principais do ciclo de seis semitons e adicionarmos uma nota um semitom acima de C, adicionaremos uma nota um semitom acima de F#. Slonimsky lita três processos de ornamentação básicos que podem ser combinados: interpolação (adicionar uma nota entre os tons principais adjacentes), ultrapolação (adicionar uma acima do próximo tom principal), infrapolação (adicionar uma nota abaixo da nota principal atual). No exemplo abaixo, retirado do livro, os três processos são ilustrados sobre o ciclo de seis semitons (sistema de duas tônicas).

Esses processos podem ser realizados com quantas notas se queira (desde que possível) – por exemplo, interpolação de 1, 2, 3, n notas – ou combinados – por exemplo inter-ultrapolação de uma nota: adicionar uma nota entre e uma acima. Abaixo um exemplo de inter-infra-ultrapolação:

É fácil perceber que, na prática, estamos construindo, sobre cada tom fundamental, a mesma classe de conjunto na mesma rotação. O que nos leva de volta à lógica dos sistemas multi-tônicas, mas tocada melodicamente. No caso acima, podemos pensar o padrão como 4-14 (9B04) construído sobre o sistema de duas tônicas considerando a terceira nota da forma normal (0 em T4 e 6 em T10) como fundamental. Parece-me que a comparação nos convida a criar padrões com mais de uma classe de conjunto e coeficientes de recorrência. No exemplo abaixo, infra-interpolo a classes 3-7 e inter-ultrapolo a classe 3-9 com coeficiente de recorrência 2 para 3-7 e 1 para 3-9.

Um adepto dos padrões melódicos de Slonimsky – não coincidentemente – é justamente Coltrane. Em sua tese, Jeff Bair estuda o uso destes padrões por Coltrane, em especial em sua última fase. Não vou transcrever as análises dele aqui, mas recomendo a leitura. Também vale escutar Interstellar Spaces de Coltrane. Vale notar que, ainda que use os padrões diretamente, parece-me que Coltrane prefere usar os ciclos como um esqueleto e preencher notas de passagem entre um e outro. Mesmo quando utiliza os padrões literalmente, Coltrane ornamenta-os com notas de passagem e aproximações típicas da linguagem do bebop, conectando a linguagem simétrica com a tradição na qual se insere.
Outra forma de pensar sistemas multi-tônicas são os modos de transposições limitadas descritos por Olivier Messiaen. Estes conjuntos de notas são estruturas simétricas que podem ser transpostas um número limitado de vezes antes de repetirem-se em conteúdo e estrutura. Por exemplo, dizemos que 3-12 (048), possui transposições limitadas pois há somente 4 transposições possíveis dele, T0, T1, T2 e T3. T4 (480) possui exatamente a mesma estrutura e classes de notas de T0 (048) ainda que em uma rotação diferente.
| 3-12 T0 (048) | 3-12 T4 (480) | 3-12 T8 (804) |
| 3-12 T1 (159) | 3-12 T5 (591) | 3-12 T9 (915) |
| 3-12 T2 (26A) | 3-12 T6 (6A2) | 3-12 T10 (A26) |
| 3-12 T3 (37B) | 3-12 T7 (7B3) | 3-12 T11 (B37) |
Os modos de transposição limitada são conjuntos de notas com a mesma propriedade. Messiaen lista sete modos e afirma ser impossível criar outros, sendo que os outros seriam subconjuntos destes. Apesar de serem sete, Messiaen prioriza na sua música os 3 primeiros, que possuem menos transposições e portanto se adequam ao seu interesse no “charme das impossibilidades”. Estes modos, diz Messiaen, “estão ao mesmo tempo na atmosfera de diversas tonalidades, sem politonalidade, deixando o compositor livre para dar predominância a uma das tonalidades ou deixar a impressão de tonalidade indecidida” (1942, p. 58).
O primeiro modo de transposição limitada é a escala de tons inteiros ou 6-35, idêntica ao ciclo de ic2, à divisão da oitava em seis partes e ao sistema de seis tônicas. Este modo possui 2 transposições e somente um modo.

O segundo modo de transposição limitada é a escala octatônica ou 8-28. Ele pode ser pensado como dois tetracordes de sétima diminuta ou 4-28 (0369). Este modo possui 3 transposições e dois modos (o que inicia com um semitom e o que inicia com um tom). No exemplo abaixo, construí os dois modos partindo de C.


O terceiro modo de transposição limitada é 9-12. Ele pode ser pensado como três tricordes aumentados ou 3-12. Este modo possui quatro transposições e três modos. Abaixo os três modos construídos sobre C.



O primeiro modo é baseado no ciclo ci2, o segundo de ci3 e o quarto de ci4. Os modos 4, 5, 6 e 7 são baseados no ciclo ci6 e são menos interessantes: possuem mais transposições e são, portanto, menos limitados. O quarto modo é 8-9 (0125678B), possui seis transposições e quatro modos. O quinto modo é 6-7 (01567B), possui seis transposições e três modos. O sexto modo é 8-25 (024568AB), possui seis transposições e quatro modos. O sétimo modo 10-6 (012356789B), possui três transposições e cinco modos.




Messiaen descreve os modos como produzidos por uma sucessão de grupos construídos sobre divisões simétricas da oitava. Por exemplo, o modo dois “é dividido em quatro grupos simétricos de três notas […] divididos em dois intervalos semitom e tom.”.

Se começarmos no segundo modo (em Db no exemplo acima) o padrão se inverte (tom, semitom), mas a estrutura simétrica se mantém. Outros tricordes construídos sobre um sistema de quatro tônicas também geram o segundo modo (e, com outras divisões, os outros modos), conectando-os aos sistemas multi-tônicas e aos padrões melódicos de Slonimsky – que, nesta visão, não passam de estruturas melódicas específicas dos modos de transposição limitada. Na versão de Messiaen, o modo é construído sobre o sistema de 4 tônicas com o tricorde 3-2A (013) ou 3-2B (023), mas podemos construí-lo, por exemplo, sobre 3-11A ou 3-11B (no exemplo abaixo).

Ou como um padrão melódico sobre a divisão de uma oitava em quatro partes. No exemplo abaixo, com inter-ultrapolação de uma nota.

O terceiro modo é produzido por sistemas e divisões baseados no ciclo de 4 semitons. Os modos 4, 5, 6 e 7 são produzidos sobre o ciclo de 6 semitons. A utilização de alguns tricordes geram versões truncadas (subconjuntos) dos modos e de alguns outros geram o total cromático.
Messiaen utiliza os modos tanto melodicamente como harmonicamente – mais especificamente como macroharmonia, ou seja, como contexto do qual extrair acordes. O exemplo aparentemente esdrúxulo que utilizei para harmonia diatônica – Lídio 7#2b6 (034678A) – pode ser pensado como um acorde de sete notas derivado do terceiro modo de transposição limitada, que poderia, dentro deste modo, ser transposto sobre o ciclo de 4 semitons mantendo a macroharmonia limitada ao modo. No exemplo abaixo, a escala na primeira expansão (E1) é construída sobre as três tônicas do ciclo de 4 semitons resultando na macroharmonia do terceiro modo, notado no sistema de baixo.

A mesma estrutura poderia ser organizada como um padrão melódico. No exemplo abaixo como infra-inter-ultrapolação. Note que a reservo a nota que começa a próximo ciclo (e que faz parte do ciclo anterior), ou seja, partindo de C, E, para a última nota do padrão – e primeira do próximo.

Um último modo de lidar com sistemas multi-tônicas são as escalas simétricas, que podem ser usadas melodicamente ou para construir harmonias diatônicas (a elas) ou diatônicas simétricas – utilizando acordes exteriores a elas. Em Symmetrical scales for jazz improvisation, Masaya Yamaguchi lista todas as escalas simétricas de duas a 10 notas – muitas das quais são simplificações ou subconjuntos dos modos de transposição limitada. Estas escalas estão descritas na tabela abaixo, pela classe de conjunto, conteúdo e equivalente.
| CC | Conteúdo | Equivalente |
| 2-6 | 06 | Complemento do 7º modo de transposição limitada/Ciclo de ci6 |
| 3-12 | 048 | Complemento do 3º modo de transposição limitada/Ciclo de ci4 |
| 4-9 | 0167 | Complemento do 4º modo de transposição limitada |
| 4-25 | 0268 | Complemento do 6º modo de transposição limitada |
| 4-28 | 0369 | Tetracorde diminuto/Ciclo de ci3 |
| 6-7 | 012678 | 5º Modo de Transposição Limitada |
| 6-20 | 014589 | Escala aumentada |
| 6-30A | 013679 | Dois tricordes menores sobre C6 |
| 6-30B | 023689 | Dois tricordes maiores sobre C6 |
| 6-35 | 02468A | 1º modo de transposição limita/Ciclo de ci2 |
| 8-9 | 01236789 | 4º modo de transposição limitada |
| 8-25 | 0124678A | 6º modo de transposição limitada |
| 8-28 | 0134679A | 2º modo de transposição limitada |
| 9-12 | 01245689A | 3º modo de transposição limitada |
| 10-6 | 01234678A | 7º modo de transposição limitada |
Todas essas escalas foram discutidas ou neste texto ou no texto sobre ciclos intervalares e não repetirei a discussão aqui. Vale dizer que todas elas podem ser construídas como classes resultantes de sistemas multi-tônicas, padrões melódicos ou como combinação de ciclos intervalares com suas transposições.
O que fazer com isso
Antes de encerrar o texto, quero propor alguns usos para explorar sistemas multi-tônicas. A ideia desses textos é produzir materiais para compor ou improvisar, mas só produzi-las não é suficiente; é preciso selecioná-los e organizá-los no tempo, pensar relações entre eles, criar materiais derivados, mapear possibilidades e depois desenvolver isso até virar música propriamente dita. Este texto olhou para parte deste processo: a construção de um contexto harmônico pela seleção de uma progressão de fundamentais e pela seleção de conjuntos a serem construídos sobre a seleção. Faltará, evidentemente, o aspecto rítmico, mas isso caberá ao leitor e à experimentação. A forma geral da música, das seções, das frases também está além do texto e será discutida em outro momento. Proponho que se tente exercitar as ideias com formas frasais bastante simples como pergunta e resposta (período) ou baixo contínuo, buscando atentar a forma como definir, num contexto não tonal, frases, interrupções, cadências e etc.
1 Progressão e acordes de passagem
Crie uma progressão selecionando uma progressão simétrica de tônicas e uma qualidade de acordes tonais, os mais tradicionais possíveis. Algo como Cmaj7, Cm7 ou C6 – talvez C7. Prefira os sistemas com poucas tônicas, isso é: os construídos sobre c3 (0369), c4 (048) e c6 (06). Isso resultaria em “esqueletos” que poderiam ser:
- Cmaj7 Ebmaj7 Gbmaj7 Amaj7
- Cm6 Em6 Abm6
- C6 Gb6
Esse esqueleto pode ser usado como uma progressão axial, uma progressão de estrutura constante ou ser preenchida com acordes de passagem ou cadenciais. A progressão axial seria seguir as progressões das tônicas literalmente, usando rotações dos acordes para uma condução de vozes parcimoniosa. A estrutura constante é uma progressão em que a mesma rotação, ou seja, o mesmo voicing, é mantido em uma progressão paralela.

Dentro de progressões axiais e estruturas constantes, do ponto de vista formal – aqui entendido como da distribuição dessa progressão no tempo – há três opções:
- Alternação constante entre as tônicas gera estase harmônica semelhante à uma harmonia modal. Em especial quando a duração das tônicas é idêntica, a progressão logo torna-se um fundo quase meditativo. Entretanto, se utilizarmos diferentes inversões dos acordes, é possível criar algum
- Outra opção com resultado meio modal é utilizar uma fundamental como tônica e as outras como ornamentações. No sistema de duas tônicas isso é simples, mas nos sistemas de três e quatro tônicas é possível ornamentar uma delas com uma estrutura e eventualmente modular para a próxima e repetir o processo.
- Distribuir assimetricamente as tônicas gera uma progressão mais contínua e funções diferentes e em cada momento para cada tônica. Isso é, uma primeira frase poderia ser Cmaj7 Abmaj7 Emaj7, onde os dois primeiros acordes duram um compasso e o último dura dois compassos; a segunda frase poderia ser Abmaj7 Emaj7 e Cmaj7 por dois compassos. A diferença de duração torna o último acorde mais próximo de uma estabilidade temporária, cria um senso de progreção e evita a ciclicidade pseudo-modal.



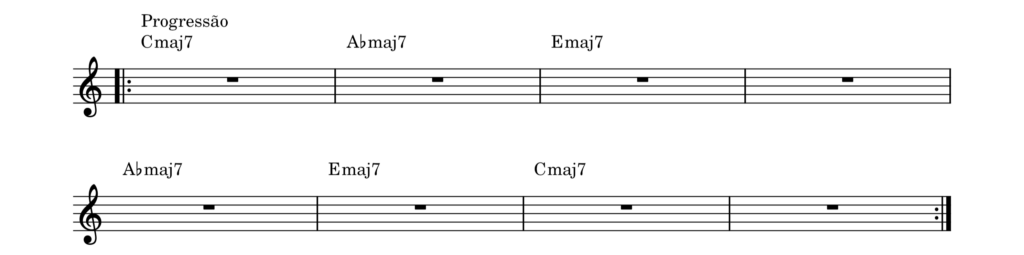
Preencher com cadências e ornamentações pode ser feito acima de qualquer uma das estruturas acima. A ideia aqui é reforçar os múltiplos centros tonais, usando fórmulas cadenciais (como ii-V-I ou IV-V-I ou mesmo iv6-I ou vi6-I) e condução de vozes. No exemplo abaixo o sistema de quatro tônicas é distribuído assimetricamente e ornamentado. Note que F# e C ocupam cada um seis tempos, enquanto A e E ocupam só 4. Isso pode fazer com que A e E soem só como ornamentações sobre um sistema de dois semitons.

O uso de sistemas multi-tônicas com cadências e ornamentações (prolongamentos etc) é a lógica por dentro de Giant Steps e por canções como Dom de Iludir de Caetano Veloso, que utiliza a mesma progressão de fundamentais, ainda que utilize cadências diferentes e uma organização menos simétrica da distribuição das fundamentais no tempo.

Este tipo de progressão acaba gerando uma linguagem mais tonal, ainda que meio errática, o que facilita comunicar a lógica de ciclos com a tradição da canção e com os materiais diatônicos que estamos acostumados a usar. Há um excelente artigo de Sérgio Freitas (2014) sobre Ciclos de terças em certas canções da música popular no Brasil descreve bem o sistema multi-tônicas e as cadências utilizadas nesta e em outras canções populares.
Vale experimentar um tratamento mais modal, seja substituindo os acordes resultantes pelos modos deles e escolher outro modo da mesma escala, seja criando progressões de modos equidistantes – ou seja, construindo um mesmo modo sobre cada uma das tônicas.
2 Construir estruturas maiores a partir de tricordes discretos
Combine os tricordes de uma progressão para formar estruturas maiores – hexacordes e complementos – e relacionar múltiplas progressões de um tricorde. Comece escolhendo um tricorde interessante, usarei 3-4A nesta seção.
Depois avalie as classes de intervalos do tricorde para escolher um ciclo a partir de um intervalo não contido. O tricorde 3-4 possui ci1, ci4 e ci5, representado no vetor classe intervalar como <1,0,0,1,1,0>. Então podemos escolher ci2, ci3 e ci6 como ciclos. Opto por esses ciclos porque classes de conjunto, quando transpostas por intervalos que não estão contidos na sua estrutura, não possuem notas em comum. T0 e T2, T0 e T3 e T0 e T6, dois a dois, não possuem notas em comum. Isso garante que o resultado entre dois conjuntos será um conjunto de cardinalidade 6.
Agora precisamos gerar as progressões. O sistema de duas tônicas, baseado em c6, gera 3-4A T0 (015) e T6 (67B). A soma dos dois tricordes – ou seja, como se fossem considerados juntos – gera 6-7 T0 (01567B), o quinto modo de transposição limitada. Podemos ou considerar isso a macro harmonia da seção e utilizá-la como escala para condução de vozes ou melodia; ou podemos usá-lo como base para gerar outra estrutura maior. Todo hexacorde possui um hexacorde complementar, ou seja, que contém as classes de notas que faltam a ele em relação à escala cromática. No caso de 6-7 T0, o complemento é 6-7 T3, que poderia ser dividido em 3-4 T3 (348) e 3-4 T9 (9A2).
| Duas tônicas | 3-4 T0 | 3-4 T6 | 6-7 T0 | |
| Complemento | 6-7 T3 | 3-4 T3 | 3-4 T9 | |
Poderíamos usar 6-7 T0 em um grupo instrumental, por exemplo nos acordes do violão, e o complementar 6-7 T3 na voz. Talvez os acordes circulem entre 3-4 T0 e T6, enquanto a voz usa 6-7 como escala mais livremente. Mas podemos também atentar ao fato de que esta matriz é um ordenamento específico do sistema de quatro tônicas: T0, T3, T6, T9. De maneira similar, os hexacordes parem progredir em c3: T0, T3… T6, T9 estão logo ali.
O sistema de quatro tônicas, baseado em c3, gera os tricordes: 3-4 T0, T3, T6 e T9. Se agruparmos os tricordes sequencialmente, isso é T0 (015) e T3 (348), T6 (67B) e T9 (9A2), geramos respectivamente 6-14A T0 (013458) e T6 (679AB2), que são complementares. Poderíamos gerar também entre T3 e T6 e T9 e T0, que resultariam na mesma classe T3 e T9, seguindo o ciclo de terças, mas a implicação da opção mais simples me interessa mais.
| Quatro tônicas | 3-4A T0 | 3-4A T3 | 3-4A T6 | 3-4A T9 |
| Soma | 6-14A T0 | 6-14A T6 | ||
| Complemento | 6-14A T6 | 6-14A T0 | ||
Poderíamos, novamente, dividir os dois hexacordes complementares, com seus tricordes, entre grupos instrumentais e etc. Ou podemos usá-los como progressão de 6-14A T0 para T6. Ou combinar ambos e ter progressões de divisões e ordenamentos específicos de toda a escala cromática. No exemplo abaixo, verticalmente temos os tricordes em c3 e horizontalmente em c6 (com seu complemento).
| 3-4A T0 | 3-4A T6 | 3-4A T3 | 3-4A T9 |
| 3-4A T3 | 3-4A T9 | 3-4A T6 | 3-4A T0 |
| 3-4A T6 | 3-4A T0 | 3-4A T3 | 3-4A T9 |
| 3-4A T9 | 3-4A T3 | 3-4A T0 | 3-4A T6 |
O ciclo de seis tônicas é construído sobre c2. Ele gera os tricordes 3-4A T0, T2, T4, T6, T8, T10. Já podemos observar que ele possui T6 em comum com os sistemas de duas e quatro tônicas. Agrupando os tricordes dois a dois e buscando os complementos, encontramos pela primeira vez um complemento que não é uma transposição, mas uma inversão do hexacorde. Neste caso, também só podemos inverter os tricordes do complemento: 6-9B não possui 3-4A, só 3-4B.
| 3-4A T0 | 3-4A T2 | 3-4A T4 | 3-4A T6 | 3-4A T8 | 3-4A T10 | |
| Soma | 6-9A T0 | 6-9A T4 | 6-9A T8 | |||
| Complemento | 6-9B T4 | 6-9B T8 | 6-9B T0 | |||
| Divisão do complemento | 3-4B T4 | 3-4B T6 | 3-4B T8 | 3-4B T10 | 3-4B T0 | 3-4B T2 |
Interessante notar que os hexacordes resultantes se movem por c4 e formam um sistema de três tônicas – o que sempre acontece quando agrupamos os tricordes do sistema de seis tônicas deste modo, suprimimos parte dele e chegamos numa versão simplificada. Poderíamos simplificar mais, agrupando 3 tricordes por vez, o que resultaria em c6.
| 3-4A T0 | 3-4A T2 | 3-4A T4 | 3-4A T6 | 3-4A T8 | 3-4A T10 | |
| Soma | 8-11A T0 | 8-11A T6 | ||||
| Complemento | 4-11B T6 (68AB) | 4-11B T0 (0245) | ||||
Como 3-4A T0 e T4 possuem uma nota em comum, em função de 3-4 possuir 1 intervalo de 4 semitons, a classe resultante da soma é um conjunto de cardinalidade 8 em vez de 9. Para gerar cardinalidade 9 precisaríamos unir só três tricordes do sistema de 4 tônicas, que gera a escala cromática. Essa combinação gera 9-4B, o complemento de 3-4A.
| Tricordes | Soma | Complemento | ||
| 3-4A T0 | 3-4A T3 | 3-4A T6 | 9-4B T11 | 3-4A T9 |
| 3-4A T3 | 3-4A T6 | 3-4A T9 | 9-4B T2 | 3-4A T0 |
| 3-4A T6 | 3-4A T9 | 3-4A T0 | 9-4B T5 | 3-4A T3 |
| 3-4A T9 | 3-4A T0 | 3-4A T3 | 9-4B T8 | 3-4A T6 |
Neste caso, poderíamos ter em um grupo de instrumentos, talvez o baixo, a guitarra ou a mão esquerda do piano, tocando 3-4A T9 e no outro grupo, talvez a voz ou a mão direita do piano, os tricordes do complemento 9-4B T11. Essa estrutura, como sugere a progressão dos complementos e das somas, seguiria c3, que poderia ser simplificada para c6, ou poderíamos misturar ciclos e criar sobre c2 3-4A e seus complementos 9-4B.
Se reunirmos as fundamentais das progressões (c2, c3 e c8) temos 8-25 T2 (0234689A), o sexto modo de transposição limitada, sobre o qual poderíamos construir com 3-4A progressões diatônica-simétricas. Se construirmos os tricordes em estrutura constante (ou seja, sem rotação), as vozes formariam 8-25 T2, T3 e T7 paralelas, que também poderiam ser pensadas como transposições possíveis de todo o sistema, assim como as transposições de 8-25 (derivada de ci6).
Podemos fazer os mesmo processos para 3-4B e gerar estruturas semelhantes, mas invertidas. Há alguns pontos em que 3-4B aparece nas estruturas que geramos com 3-4A: 6-7A contém tanto 3-4A quanto 3-4B (e o mesmo vale para 3-4B); 6-14A também; 6-9A se complementa com 6-9B, sendo que o primeiro só contém 3-4A e o segundo 3-4B. Essas conexões poderiam ser pensadas como pivôs entre sistemas de 3-4A e sistemas de 3-4B para gerar “modulações” entre os dois sistemas.
Geramos uma rede de materiais que podem ser usados ao gosto do compositor ou improvisador para estruturar progressões como as discutidas na seção anterior. A partir do tricorde e dos ciclos, geramos escalas de fundamentais, complementos, hexacordes e complementaridade hexacordal, progressões de hexacordes, octacordes, nonacordes e da escala cromática como um todo.
Em termos de ciclo, partimos de c2, c3 e c6, mas encontramos, a partir de c2, c4 como ciclo possível para os hexacordes. Como hexacordes, encontramos 6-7 (derivado de c6 e que pode ser ampliado com c3), 6-14A (derivado de c3, gerando c6), 6-9A (derivado de C2) e seu complemento 6-9B. Dois octacordes: 8-11A, gerado a partir de c2 agrupado em 3 tricordes e 8-25 como escala das fundamentais. Por fim, como complemento a 3-4A, 9-4B. Tente explorar essa relações em uma progressão, dividindo e combinando verticalmente e horizontalmente as estruturas geradas.
3 Combinar ciclos
Outra opção é usar os ciclos intercaladamente com coeficientes de interferência do mesmo modo que fizemos com as progressões diatônicas. Isso gera, o que Keith Waters chama de progressão axial dupla:
Uma progressão axial dupla surge através de pares de acordes transpostos sistematicamente. Por exemplo, nos compassos 21–24 de Moontrane, de Woody Shaw, ocorre uma progressão mais ampla baseada no eixo de terça menor, formada pelos acordes Gm7–Fm7–B♭m7–A♭m7–C♯m7–Bm7. Essa progressão de duplo eixo é indicada neste livro como m3 (−M2, +P4): m3 representa o movimento entre os dois eixos harmônicos, enquanto os valores entre parênteses indicam a direção (+ para cima, − para baixo) e a distância entre as harmonias consecutivas dentro de cada par.
Progressões axiais duplas geram pequenas células que se repetem em uma progressão maior. No exemplo acima c10 (ciclo segunda menor descendente) e c5 (ciclo de quarta justa) combinam-se para formar c3 (ciclo de terças menores ascendentes). A célula gera uma progressão de fundamentais que corresponde à classe 3-7A T10 (A03) e que repete-se sobre c3. Observe que, como conjunto ordenado (ou seja 0A3) a última nota da primeira célula é a primeira da segunda célula (316) e assim por diante.
Utilizando o tricorde e os ciclos da seção anterior (3-4A e c2, c3 e c4) podemos gerar combinações binomiais, trinomiais e polinomiais entre os ciclos. Com esses intervalos é possível gerar seis progressões binomiais, que geram as células de fundamentais 3-7A e 3-7B (sobre c5), duas rotações de 3-8A (sobre c8) e duas rotações de 3-10 (sobre c9).

Também é possível gerar seis progressões trinomiais, que geram células de cardinalidade 4 repetindo-se sobre c11: 4-12A, 4-13A, 4-13B, 4-Z15A e 4-Z15B.

Diferentemente das progressões binomiais, as progressões trinomiais – geradas pelos intervalos selecionados pelo processo da seção anterior – geram células que possuem a mesma extensão (11 semitons neste caso) e, portanto, repetem-se sempre sobre o mesmo ciclo. Isso tem duas implicações:
- É possível estruturar uma progressão geral sobre c11 (0BA98…) e a cada fundamental desta progressão selecionar uma célula diferente. Pode-se escolhê-las aleatoriamente, ou criar alguma regra de seleção e recorrência para cada célula. De qualquer modo, isso mantém a continuidade (sobre c11), mas produz maior variação. No exemplo abaixo, a progressão c11 é notada com cabeça vazada e os tetracordes são variados entre elas.

- É possível desconsiderar a última nota da célula e simplificar a progressão: em vez de 4-13A sobre c11, podemos nos referir a 3-7A sobre c11, obtendo o mesmo resultado. No exemplo abaixo, uma mesma progressão de fundamentais é notada como 3-7A sobre c11 e como 4-13A sobre c11.

A vantagem de notar com tricordes, como tenho insistido, é que é mais fácil pensar com eles: há menos conjuntos de cardinalidade 3 (12 classes em comparação com as 29 de cardinalidade 4), eles são mais simples e é mais fácil de combiná-los em estruturas maiores.
Falando em combinar tricordes, como fizemos na seção anterior, podemos agrupar os tricordes discretos e criar progressões de hexacordes. Na progressão acima, por exemplo, temos 3-4A T0 (015) + T2 (237) formando 6-9A T0 (012357) seguido de 3-4A T5 (56A) + 3-4A T11 (B04) formando 6-7 T4 (456AB0) e assim sucessivamente.
| Tricordes | 3-4A T0 | 3-4A T2 | 3-4A T5 | 3-4A T11 | 3-4A T1 | 3-4A T4 | 3-4A T10 | 3-4A T0 |
| Soma | 6-9A T0 (012357) | 6-7 T4 (456AB0) | 6-14A T1 (124569) | 6-9A T10 (AB0135) | ||||
Se tratarmos os tricordes somados como dois grupos instrumentais diferentes, temos progressões diferentes em cada voz e uma progressão geral dos hexacordes. O mesmo pode ser feito também com o complemento, de modo que a progressão mova ordenamentos de toda a escala cromática.
| 2º tricorde | 3-4A T2 | 3-4A T11 | 3-4A T4 | 3-4A T0 |
| 1º tricorde | 3-4A T0 | 3-4A T5 | 3-4A T1 | 3-4A T10 |
| Soma | 6-9A T0 (012357) | 6-7 T4 (456AB0) | 6-14A T1 (124569) | 6-9A T10 (AB0135) |
Evidentemente, também é possível criar progressões polinomiais, com polinômios tanto para a progressão das fundamentais, como por exemplo 1C2 + 2C3, quanto para as estruturas, por exemplo 2 3-4A + 3-7A. Ainda podemos interferir os polinômios e criar progressões maiores.
4 Usar parcialmente, superimpor ou usar como enquadramento e preencher
Para acabar este texto de uma vez, vou apontar rapidamente mais alguns usos:
- Excetuando os sistemas de duas e três tônicas, é possível usar as progressões em parte, sem a necessidade de completar o ciclo ou uma progressão progressão polinomial. O uso parcial deixa a progressão menos óbvia e pode ser usada mesmo como o que o Philip Tagg chama de chord shuffle.
- Num contexto modal ou tonal, podemos super impor as sistemas axiais parciais sobre a progressão. Um exemplo interessante que Rick Beato propõe no Beato Book é superimpor um sistema de seis tônicas parcial sobre um blues de 12 compassos. Aqui as rearmonizações de Coltrane são o exemplo paradigmático e recomendo a leitura de John Coltrane Plays “Coltrane Changes” Songbook de Masaya Yamaguchi. Superimpor é sair com o objetivo de voltar – num contexto como no blues, voltar para os acorde chave (I7,IV7 e V7) aproximadamente nas posições importantes (1º, 5º e 9º compassos). Num contexto modal, voltar aos acordes primários e ao modo específico. É importante manter a frase e usar a superimposição para aproximar cromaticamente as notas alvo. Liebmann sugere nem seguir um ciclo contínuo, nem utilizar acordes constantes pra evitar monotonia e previsibilidade. Superimpor progressões polinomiais pode dar conta disso.
- Usar a progressão simétrica de fundamentais como enquadramento e preencher com acordes, arpejos, classes de conjunto, fragmentos melódicos ou para desenvolver licks previamente desenvolvidos na sua linguagem. Isso é, abandonar preocupações formais em favor de uma linguagem simétrica que tem as divisões da oitava (ou seja, as tônicas) como meta tonal, em vez de ter a macroharmonia como objeto.,
- Usando uma estrutura constante de classes de notas (por exemplo a escala diatônica ou 7-35) construída sobre uma progressão de fundamentais, mas alterando a tônica. Podemos usar, por exemplo, um sistema de 3 tônicas (C Eb G#) e gerar, por exemplo:
- Construíndo a escala maior sobre cada uma das tônicas e usando seus modos: C jônio (C maior), C eólio (Eb maior), C# lídio (G# maior), A eólio (C maior), Ab lídio (Eb maior) e assim por diante.
- Construíndo modos da escala maior diferentes em cada tônica: C jônio, Eb eólio, G# lídio etc.
Referências
Bair, Jeff, Cyclic Patterns in John Coltrane’s Melodic Vocabulary as Influenced by Nicolas Slonimsky’s Thesaurus of Scales and Melodic Patterns: An Analysis of Selected Improvisations. Doctor of Musical Arts (Performance).
Freitas, S. P. R. D. (2014). Ciclos de terças em certas canções da música popular no Brasil. Per musi, 125-146.
Hannaford, M. E. (2023). Theory on the South Side: Muhal Richard Abrams’s Engagement with Joseph Schillinger’s System of Musical Composition. Journal of the Society for American Music, 17(1), 43-67.
Messiaen, Olivier (1942). The Technique of my Musical Language, Paris: Alphonse LeDuc.
Rochinski S. (2022). Modern Jazz Theory and Practice: The Post-Bop Era. Berklee Press.
Slonimsky, Nicolas (1947). Thesaurus of Scales and Melodic Patterns. New York:Schirmer Books.
Schillinger, Joseph (1946) The Schillinger system of musical composition. New York: Carl Fische
Waters, K. (2019). Postbop Jazz in the 1960s: The Compositions of Wayne Shorter, Herbie Hancock, and Chick Corea. Oxford University Press.