Eu comecei este blog com a expectativa de produzir pequenos textos focados em um conceito específico apresentados de modo que fossem facilmente aplicáveis. Escrever os dois textos que postei até agora me mostraram que isso provavelmente não vai ser o caso. Está claro que deve haver pelo menos dois tipos de texto: textos longos explorando conceitos básicos e alguma outra coisa que seja mais curta, mais diretamente prática. Pensando nisso e no fato de que escrevi os dois primeiros textos para serem enterradas em outros assuntos que combinassem os dois, resolvi começar a escrever, em paralelo, um tipo diferente de textos que vou chamar de Interferências.
A noção de interferência vêm do Sistema Schillinger de Composição Musical e sozinha daria uma série de textos que podem ser escritos no futuro, mas achei que valia roubá-la como título para esta série e, em uma versão adaptada, usá-la como base para este texto. De maneira muito simplificada, uma interferência, no sistema Schillinger, é uma combinação entre dois (ou mais) pulsos periódicos que resultam em uma estrutura rítmica nova.
Chamarei estes textos de interferências para marcar o fato de que, nelas, trata-se de fazer interagir, combinar, afetar mutuamente dois ou mais conceitos básicos de textos longos para produzir coisas novas e, de preferência, rapidamente aplicáveis. Achei apropriado começar primeira Interferência usando a noção de interferência, mas aplicada aos Ciclos intervalares na produção de tricordes, famílias de tricordes, redes de simultaneidades e etc.
Este texto foi publicado com um complemento: um PDF contendo todas as transposições e relações das interferências discutidas neste texto. Além de ser mais completo, o documento possui as tabelas com mais qualidade. Não sei se é pura ignorância minha, mas não dei jeito de formatá-las direito nesta publicação e acabei usando prints em alguns casos. O complemento pode ser acessado aqui.
Problema
Este texto é motivado por um problema bastante prático: temos 19 tricordes, 43 tetracordes, 66 pentacordes e assim por diante, cada um com 12 transposições, certo número de rotações e aberturas a depender da cardinalidade… qualquer um deles pode, em princípio, seguir-se de qualquer outro e depois qualquer outro… manter a coerência de uma música ou mesmo de uma parte dela depende de limitar a quantidade de conjuntos utilizados e criar relações sonoras entre eles. Há inúmeras formas de fazê-lo, algumas por propriedades intrínsecas dos conjuntos, alguns por lógicas extrínsecas, alguns informados por um resultado sonoro a ser expandido, outros por um objetivo a ser atingido. Neste texto, vou explorar uma forma de reduzir a quantidade de tricordes e relacioná-los uns aos outros através da sua produção por ciclos intervalares para criar uma espécie de “campo harmônico”, ou pelo menos um campo limitado de possibilidades expansíveis de encadeamento de simultaneidades pós-tonais. Também espero que seja um exercício divertido relacionando o texto sobre Ciclos Intervalares e o texto sobre Conjuntos de Classes de Notas.
Interferência entre Ciclos Intervalares
Para tanto, vamos trabalhar com interferências entre dois ciclos de notas. Por interferência quero dizer: partindo da mesma nota (e nos nossos exemplos sempre C ou 0), construímos dois ciclos até eles se reencontrarem em outra nota comum e combinando as classes de notas de ambos na ordem em que aparecem. A interferência entre o ciclo de 2 e o ciclo de 3 semitons (que chamarei de 3:2, seguindo o padrão de Schillinger) gera a seguinte resultante (r)
a: 036
b: 0246
r: 02346
Observe que os ciclos continuariam, ambos repetindo-se após uma oitava, mas paramos a resultante no primeiro encontro entre eles após o ponto de partida. Poderíamos continuar, mas o ciclo teria a mesma estrutura intervalar (2,1,1,2) partindo de 6 e, para simplificar, preferirei utilizar a versão mais simples – i.e. mais compacta – de cada ciclo.
Interferências dos ciclos de intervalos simples
Para gerar as interferências, construímos os dois ciclos componentes (a e b) até que eles atinjam o MMC. Isso geralmente supera uma oitava, então é mais fácil começarmos somando inteiros e depois reduzir para uma oitava pela operação de módulo 12. Depois juntamos, na ordem ascendente dos inteiros, os dois ciclos. Por exemplo:
6:5 (MMC: 30)
a: 0 6 12 24 30
b: 0 5 10 15 20 25 30
r: 0 5 6 10 12 15 20 24 25 30
Em seguida, reduzimos tudo para módulo 12, de modo que 6:5 gera um conjunto ordenado, ascendente: 0 5 6 A 0 3 6 8 0 1 6.
Incluirei nesta publicação somente a versão reduzida a módulo 12 das interferências não-triviais. Caso queira consultar todas as interferências e as interferências sem módulo 12, elas estão disponíveis neste arquivo.
| Interferências não triviais (módulo 12) | |||||||||||||||||||||
| 3:2 | 0 | 2 | 3 | 4 | 6 | ||||||||||||||||
| 4:3 | 0 | 3 | 4 | 6 | 8 | 9 | 0 | ||||||||||||||
| 5:2 | 0 | 2 | 4 | 5 | 6 | 8 | 10 | ||||||||||||||
| 5:3 | 0 | 3 | 5 | 6 | 9 | 10 | 0 | 3 | |||||||||||||
| 5:4 | 0 | 4 | 5 | 8 | 10 | 0 | 3 | 4 | 8 | ||||||||||||
| 6:4 | 0 | 4 | 6 | 8 | 0 | ||||||||||||||||
| 6:5 | 0 | 5 | 6 | 10 | 0 | 3 | 6 | 8 | 0 | 1 | 6 | ||||||||||
| 7:2 | 0 | 2 | 4 | 6 | 7 | 8 | 10 | 0 | 2 | ||||||||||||
| 7:3 | 0 | 3 | 6 | 7 | 9 | 0 | 2 | 3 | 6 | 9 | |||||||||||
| 7:4 | 0 | 4 | 7 | 8 | 0 | 2 | 4 | 8 | 9 | 0 | 4 | ||||||||||
| 7:5 | 0 | 5 | 7 | 10 | 2 | 3 | 8 | 9 | 1 | 4 | 6 | 11 | |||||||||
| 7:6 | 0 | 6 | 7 | 0 | 2 | 6 | 9 | 0 | 4 | 6 | 11 | 0 | 6 | ||||||||
| 8:3 | 0 | 3 | 6 | 8 | 9 | 0 | 3 | 4 | 6 | 9 | 0 | ||||||||||
| 8:5 | 0 | 5 | 8 | 10 | 3 | 4 | 8 | 0 | 1 | 6 | 8 | 11 | 4 | ||||||||
| 8:6 | 0 | 6 | 8 | 0 | 4 | 6 | 0 | ||||||||||||||
| 8:7 | 0 | 7 | 8 | 2 | 4 | 9 | 0 | 4 | 8 | 11 | 4 | 6 | 0 | 1 | 8 | ||||||
| 9:2 | 0 | 2 | 4 | 6 | 8 | 9 | 10 | 0 | 2 | 4 | 6 | ||||||||||
| 9:4 | 0 | 4 | 8 | 9 | 0 | 4 | 6 | 8 | 0 | 3 | 4 | 8 | 0 | ||||||||
| 9:5 | 0 | 5 | 9 | 10 | 3 | 6 | 8 | 1 | 3 | 6 | 11 | 0 | 4 | 9 | |||||||
| 9:6 | 0 | 6 | 9 | 0 | 6 | ||||||||||||||||
| 9:7 | 0 | 7 | 9 | 2 | 6 | 9 | 3 | 4 | 11 | 0 | 6 | 9 | 1 | 6 | 8 | 3 | |||||
| 9:8 | 0 | 8 | 9 | 4 | 6 | 0 | 3 | 8 | 0 | 4 | 9 | 0 | 6 | 8 | 3 | 4 | 0 | ||||
| 10:3 | 0 | 3 | 6 | 9 | 10 | 0 | 3 | 6 | 8 | 9 | 0 | 3 | 6 | ||||||||
| 10:4 | 0 | 4 | 8 | 10 | 0 | 4 | 8 | ||||||||||||||
| 10:6 | 0 | 6 | 10 | 0 | 6 | 8 | 0 | 6 | |||||||||||||
| 10:7 | 0 | 7 | 10 | 2 | 8 | 9 | 4 | 6 | 11 | 4 | 6 | 1 | 2 | 8 | 0 | 3 | 10 | ||||
| 10:8 | 0 | 8 | 10 | 4 | 8 | 0 | 6 | 8 | 4 | ||||||||||||
| 10:9 | 0 | 9 | 10 | 6 | 8 | 3 | 6 | 0 | 4 | 9 | 2 | 6 | 0 | 3 | 10 | 0 | 8 | 9 | 6 | ||
| 11:2 | 0 | 2 | 4 | 6 | 8 | 10 | 11 | 0 | 2 | 4 | 6 | 8 | 10 | ||||||||
| 11:3 | 0 | 3 | 6 | 9 | 11 | 0 | 3 | 6 | 9 | 10 | 0 | 3 | 6 | 9 | |||||||
| 11:4 | 0 | 4 | 8 | 11 | 0 | 4 | 8 | 10 | 0 | 4 | 8 | 9 | 0 | 4 | 8 | ||||||
| 11:5 | 0 | 5 | 10 | 11 | 3 | 8 | 10 | 1 | 6 | 9 | 11 | 4 | 8 | 9 | 2 | 7 | |||||
| 11:6 | 0 | 6 | 11 | 0 | 6 | 10 | 0 | 6 | 9 | 0 | 6 | 8 | 0 | 6 | 7 | 0 | 6 | ||||
| 11:7 | 0 | 7 | 11 | 2 | 9 | 10 | 4 | 9 | 11 | 6 | 8 | 1 | 7 | 8 | 3 | 6 | 10 | 5 | |||
| 11:8 | 0 | 8 | 11 | 4 | 10 | 0 | 8 | 9 | 4 | 8 | 0 | 7 | 8 | 4 | 6 | 0 | 5 | 8 | 4 | ||
| 11:9 | 0 | 9 | 11 | 6 | 10 | 3 | 9 | 0 | 8 | 9 | 6 | 7 | 3 | 6 | 0 | 5 | 9 | 4 | 6 | 3 | |
| 11:10 | 0 | 10 | 11 | 8 | 10 | 6 | 9 | 4 | 8 | 2 | 7 | 0 | 6 | 10 | 5 | 8 | 4 | 6 | 3 | 4 | 2 |
Algumas propriedades das interferências entre ciclos intervalares
As interferências (tanto intervalares como rítmicas) repetem-se, como vimos anteriormente, após um intervalo específico. Este intervalo é sempre o mínimo múltiplo comum dos intervalos básicos dos ciclos componentes da interferência. No caso de 2 e 3, 6. No caso de 3 e 5, 15… e assim por diante. Em alguns casos, esse intervalo é a oitava, como em 3 e 4 (12), ou uma oitava composta, como 3 e 8 (24). Mas, geralmente, não é: a oitava é só um caso de repetição e equivalência entre outros.
Algumas interferências são truncamentos de ciclos e vou considerá-las irrelevantes. Por exemplo, a interferência 6:3 gera 036, que é simplesmente o ciclo de 3 semitons incompleto. Todas as interferências entre números que são múltiplos um do outro geram ciclos intervalares incompletos e serão consideradas triviais. Na prática, outras interferências, como 9:6 também resultam em ciclos incompletos, mas as manti porque não se encaixavam na fórmula que usei para filtrá-las, isso é: numa interferência n:m, se m módulo n = 0.
Cada interferência é um conjunto ordenado de classes de notas, como uma série dodecafônica. Deste modo, ele pode ser descrito por uma estrutura intervalar ordenada (uma sequência de intervalos ascendentes). A interferência 3:2, por exemplo, possui uma estrutura 2 1 1 2, isso é, começando em 0, sobe dois semitons para 2, um para 3, um para 4 e dois para 6.
A estrutura intervalar de uma interferência pode ser transpostas, de modo que a interferência pode ser construída iniciando em qualquer classe de nota. Para diferenciar a interferência abstrata e a interferência concreta (numa transposição específica), vou me referir à classe de interferência e interferência. Classe de interferência é o conjunto das interferências que possuem a mesma estrutura intervalar – ou seja, são criadas pela mesma combinação de ciclos intervalares – em todas as transposições. Vou me referir a elas como n:m (3:2, 5:4, etc), sendo que m é o ciclo menor. As interferências concretas são as transposições específicas e vou me referir a elas como n:m To, onde n:m é a classe de interferência e To descreve a transposição (o sendo o intervalo ao qual ela é transposta a partir de 0).
A estrutura intervalar de uma interferência n:m sempre possui somente intervalos menores ou iguais a m (intervalo do ciclo menor). Por exemplo: 6:4, possui é composta pelos intervalos 4, e 2. Por fim,t odos os ciclos são simétricos em volta de um ponto central, ou seja, possuem a mesma estrutura intervalar “subindo” ou “descendo”.
Tricordes Consecutivos
As interferências podem ser usadas melódica ou harmonicamente, em partes ou em sua totalidade, do modo que o compositor achar apropriado. Neste texto, entretanto, me interessa segmentá-las em tricordes. Para isso, é preciso pegar emprestado da linguagem dodecafônica o termo tricordes consecutivo. Uma série dodecafônica é um conjunto ordenado de 12 notas, por exemplo: 0123456789AB. Qualquer conjunto ordenado de 12 notas pode ser dividido em uma sequência de 4 conjuntos de 3 notas sem notas em comum chamados tricordes contínuos, no nosso caso: 012 | 345 | 678 | 9AB. Ele também pode ser dividido em uma sequência de 10 conjuntos de 3 notas, no nosso exemplo: 012 | 123 | 234 | […] 89A | 9AB. Estes são os tricordes consecutivos da série. No dodecafonismo, tricordes discretos e consecutivos são usados para descrever a série e analisar certas propriedades geradas pro elas, como a saturação motívica da mesma.
Tratarei as interferências do mesmo modo: dividindo-as em tricordes consecutivos para gerar a família de tricordes relacionadas através da interferência. Por exemplo 5:3 (03569A03) gera os tricordes consecutivos: 035 | 356 | 569 | 69A | 9A0 | A03. Na tabela, todas as interferências não-triviais foram divididas em tricordes.
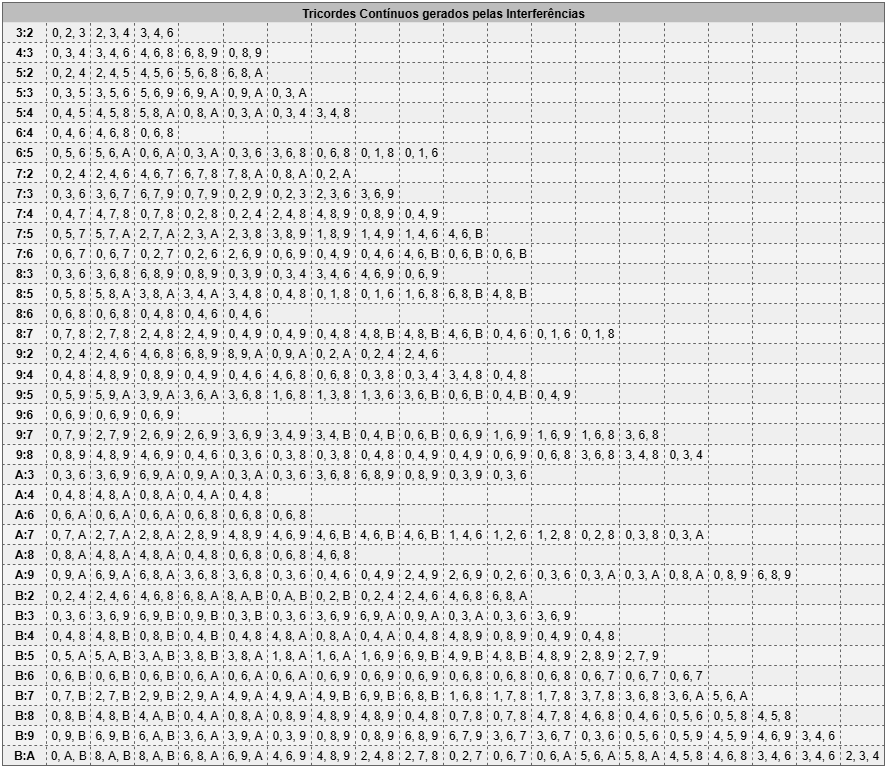
Obviamente, esta é uma forma desnecessariamente específica de notar os tricordes. Na tabela abaixo, optei por notá-las usando a notação de conjuntos (Classe, transposição). Neste caso, nosso exemplo 5:3 contém os tricordes: 3-7 I0, 3-2 I3, 3-3 T5, 3-3 I6, 3-2 T9 e 3-7 T10. O que, parece-me, é mais fácil de transpor para interferências começando em outras classes de notas.
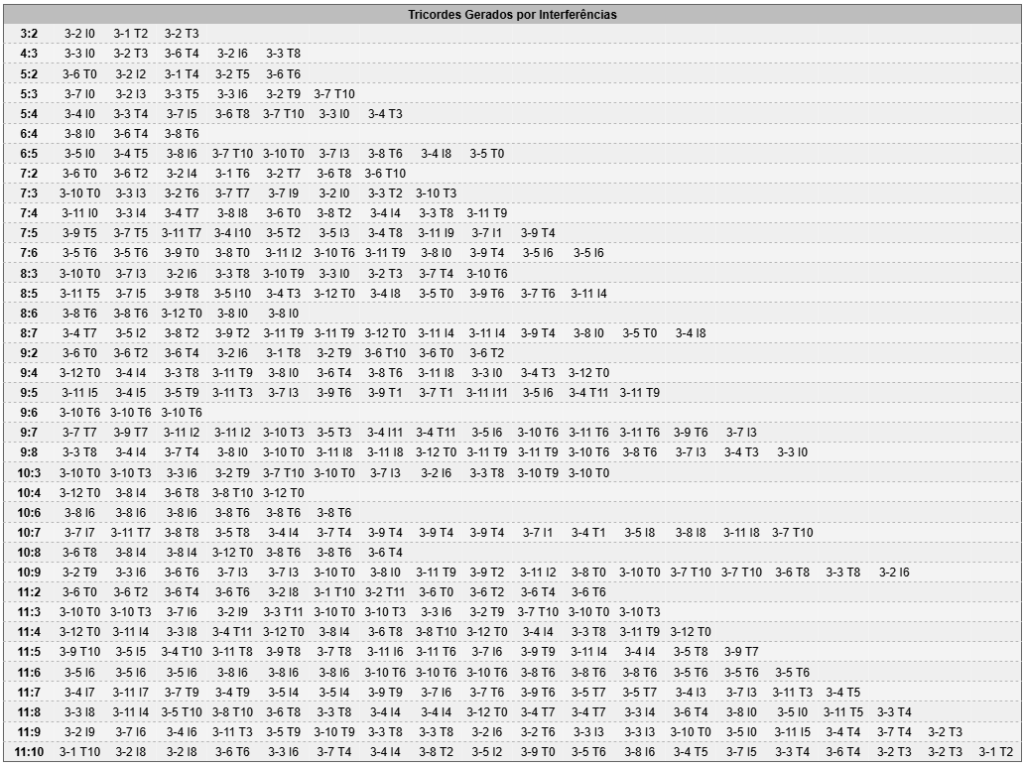
Observe que, em função da simetria das interferências, o primeiro e o último, o segundo e o penúltimo e (assim sucessivamente) tricordes são inversões um do outro (quando possível), de modo que, excetuando no caso de haver um tricorde central, cada classe de conjunto aparece pelo menos duas vezes no ciclo.
Relações entre Interferências
Ainda assim, esta forma de notar pode ser simplificada para identificar melhor o conteúdo de tricordes das interferências. Na tabela abaixo, reduzi a tabela acima, removendo inversões e transposições e mantendo somente que tipos de Classes de Conjunto são produzidas por cada classe de interferência.
| Classes de Conjunto Geradas por Cada Interferência | |||||||||
| 3:2 | 3-2 | 3-1 | |||||||
| 4:3 | 3-3 | 3-2 | 3-6 | ||||||
| 5:2 | 3-6 | 3-2 | 3-1 | ||||||
| 5:3 | 3-7 | 3-2 | 3-3 | ||||||
| 5:4 | 3-4 | 3-3 | 3-7 | 3-6 | |||||
| 6:4 | 3-8 | 3-6 | |||||||
| 6:5 | 3-5 | 3-4 | 3-8 | 3-7 | 3-10 | ||||
| 7:2 | 3-6 | 3-2 | 3-1 | ||||||
| 7:3 | 3-10 | 3-3 | 3-2 | 3-7 | |||||
| 7:4 | 3-11 | 3-3 | 3-4 | 3-8 | 3-6 | ||||
| 7:5 | 3-9 | 3-7 | 3-11 | 3-4 | 3-5 | ||||
| 7:6 | 3-5 | 3-9 | 3-8 | 3-11 | 3-10 | ||||
| 8:3 | 3-10 | 3-7 | 3-2 | 3-3 | |||||
| 8:5 | 3-11 | 3-7 | 3-9 | 3-5 | 3-4 | 3-12 | |||
| 8:6 | 3-8 | 3-12 | |||||||
| 8:7 | 3-4 | 3-5 | 3-8 | 3-9 | 3-11 | 3-12 | |||
| 9:2 | 3-6 | 3-2 | 3-1 | ||||||
| 9:4 | 3-12 | 3-4 | 3-3 | 3-11 | 3-8 | 3-6 | |||
| 9:5 | 3-11 | 3-4 | 3-5 | 3-7 | 3-9 | ||||
| 9:6 | 3-10 | ||||||||
| 9:7 | 3-7 | 3-9 | 3-11 | 3-10 | 3-5 | 3-4 | |||
| 9:8 | 3-3 | 3-4 | 3-7 | 3-8 | 3-10 | 3-11 | 3-12 | ||
| 10:3 | 3-10 | 3-3 | 3-2 | 3-7 | |||||
| 10:4 | 3-12 | 3-8 | 3-6 | ||||||
| 10:6 | 3-8 | ||||||||
| 10:7 | 3-7 | 3-11 | 3-8 | 3-5 | 3-4 | 3-9 | |||
| 10:8 | 3-6 | 3-8 | 3-12 | ||||||
| 10:9 | 3-2 | 3-3 | 3-6 | 3-7 | 3-10 | 3-8 | 3-11 | 3-9 | |
| 11:2 | 3-6 | 3-2 | 3-1 | ||||||
| 11:3 | 3-10 | 3-7 | 3-2 | 3-3 | |||||
| 11:4 | 3-12 | 3-11 | 3-3 | 3-4 | 3-8 | 3-6 | |||
| 11:5 | 3-9 | 3-5 | 3-4 | 3-11 | 3-7 | ||||
| 11:6 | 3-5 | 3-8 | 3-10 | ||||||
| 11:7 | 3-4 | 3-11 | 3-7 | 3-5 | 3-9 | ||||
| 11:8 | 3-3 | 3-11 | 3-5 | 3-8 | 3-6 | 3-4 | 3-12 | ||
| 11:9 | 3-2 | 3-7 | 3-4 | 3-11 | 3-5 | 3-10 | 3-3 | ||
| 11:10 | 3-1 | 3-2 | 3-6 | 3-3 | 3-7 | 3-4 | 3-8 | 3-5 | 3-9 |
Notadas deste modo, é mais fácil de observar qual o conteúdo de classes de notas – e consequentemente a sonoridade – de cada classe de interferência. A interferência 5:4, por exemplo, possui os tricordes 3-3 e 3-4 (acordes mistos de semitom), o tricorde 3-7 (acorde misto pentatônico) e 3-6 (acorde secundal de tons inteiros).
Observe também que cada tricorde participa de (ou é gerado por) diversas interferências. Se imaginarmos que uma interferência gera um campo de possibilidades harmônicas – reduzida a um conjunto de classes de conjunto em transposições específicas – os tricordes compartilhados por mais de uma interferência funcionariam como acordes pivot entre duas interferências. Na tabela abaixo, organizei as interferências a partir dos tricordes que gera. O tricorde 3-1, por exemplo, participa das interferências 3:2, 5:2, 7:2, 9:2, 11:2 e 10:2.
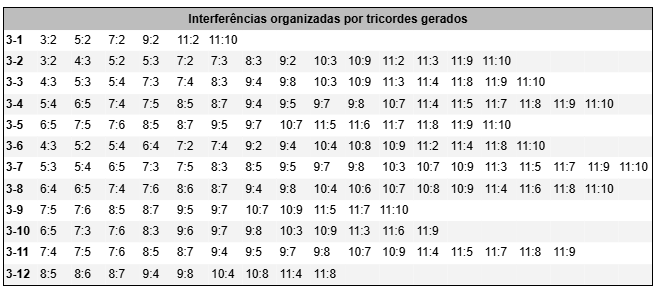
Além de tricordes comuns (ou pivot), as interferências podem possuir outra coisa em comum: o conjunto resultante. Na tabela abaixo, listo as interferências e as classes de conjunto resultantes de cada uma.

Obviamente, podemos organizar esta informação ao contrário. Ou seja, partindo da classe resultante (independente da transposição), quais interferências resultam nela. Ainda que algumas Classes sejam geradas por somente uma interferência, aquelas que são geradas por múltiplas interferências possuem, em potencial, duas organizações diferentes de tricordes.
| Interferências por Classe Resultante | ||||
| 3-10 T | 9:6 | |||
| 4-21 T | 10:6 | |||
| 4-24 T | 6:4 | 8:6 | 10:4 | |
| 5-33 T | 10:8 | |||
| 5-8 T | 3:2 | |||
| 6-Z28 T | 4:3 | 8:3 | 9:4 | 9:8 |
| 6-Z29 T | 5:3 | 7:3 | ||
| 6-Z37 T | 11:4 | |||
| 6-Z42 T | 11:3 | |||
| 6-Z45 T | 10:3 | |||
| 6-Z48 T | 5:4 | 7:4 | ||
| 7-1 T | 11:6 | |||
| 7-33 T | 5:2 | 7:2 | 9:2 | 11:2 |
| 7-35 T | 6:5 | 7:6 | ||
| 8-25 T | 10:9 | |||
| 9-1 T | 11:8 | |||
| 9-9 T | 8:5 | 8:7 | ||
| 10-1 T | 11:9 | |||
| 10-5 T | 9:5 | 9:7 | ||
| 11-1 T | 10:7 | 11:10 | ||
| 12-1 T | 7:5 | 11:5 | 11:7 | |
| Tricordes gerados pelas Interferências de cada Classe de Conjunto | |||||||||
| 4-24 T | |||||||||
| 6:4 | 3-8 | 3-6 | |||||||
| 8:6 | 3-8 | 3-12 | |||||||
| 10:4 | 3-12 | 3-8 | 3-6 | ||||||
| 6-Z28 T | |||||||||
| 4:3 | 3-3 | 3-2 | 3-6 | ||||||
| 8:3 | 3-10 | 3-7 | 3-2 | 3-3 | |||||
| 9:4 | 3-12 | 3-4 | 3-3 | 3-11 | 3-8 | 3-6 | |||
| 9:8 | 3-3 | 3-4 | 3-7 | 3-8 | 3-10 | 3-11 | 3-12 | ||
| 6-Z29 T | |||||||||
| 5:3 | 3-7 | 3-2 | 3-3 | ||||||
| 7:3 | 3-10 | 3-3 | 3-2 | 3-7 | |||||
| 6-Z48 T | |||||||||
| 5:4 | 3-4 | 3-3 | 3-7 | 3-6 | |||||
| 7:4 | 3-11 | 3-3 | 3-4 | 3-8 | 3-6 | ||||
| 7-33 T | |||||||||
| 5:2 | 3-6 | 3-2 | 3-1 | ||||||
| 7:2 | 3-6 | 3-2 | 3-1 | ||||||
| 9:2 | 3-6 | 3-2 | 3-1 | ||||||
| 11:2 | 3-6 | 3-2 | 3-1 | ||||||
| 7-35 T | |||||||||
| 6:5 | 3-5 | 3-4 | 3-8 | 3-7 | 3-10 | ||||
| 7:6 | 3-5 | 3-9 | 3-8 | 3-11 | 3-10 | ||||
| 9-9 T | |||||||||
| 8:5 | 3-11 | 3-7 | 3-9 | 3-5 | 3-4 | 3-12 | |||
| 8:7 | 3-4 | 3-5 | 3-8 | 3-9 | 3-11 | 3-12 | |||
| 10-5 T | |||||||||
| 9:5 | 3-11 | 3-4 | 3-5 | 3-7 | 3-9 | ||||
| 9:7 | 3-7 | 3-9 | 3-11 | 3-10 | 3-5 | 3-4 | |||
| 11-1 T | |||||||||
| 10:7 | 3-7 | 3-11 | 3-8 | 3-5 | 3-4 | 3-9 | |||
| 11:10 | 3-1 | 3-2 | 3-6 | 3-3 | 3-7 | 3-4 | 3-8 | 3-5 | 3-9 |
| 12-1 T | |||||||||
| 7:5 | 3-9 | 3-7 | 3-11 | 3-4 | 3-5 | ||||
| 11:5 | 3-9 | 3-5 | 3-4 | 3-11 | 3-7 | ||||
| 11:7 | 3-4 | 3-11 | 3-7 | 3-5 | 3-9 | ||||
Um exemplo simples são as interferências que geram 4-24 (6:4, 8:6 e 10:4). Os três ciclos transpostos para gerar 4-24 T4 (4680) dividem 3 tipos de tricordes entre si, sendo que esses tricordes estão na mesma transposição 3-6 T4, 3-8 T6 e 3-8 I0 e 3-12 T0. 6:4 possui só 3-6 e 3-8; 8:6 possui só 3-8 e 3-12 e 10:4 possui os três tricordes.
Entretanto, há diferenças quando consideramos o módulo, isso é, onde a interferência se repete. As interferências 6:4 e 8:6 repetem-se a cada oitava (composta no caso de 8:6 e simples de 6:4), mas 10:4 repete-se a cada 8 semitons. Se continuássemos a interferência, após o fechamento do primeiro módulo, a próxima iteração de 10:4 aconteceria sobre 4-24 T0 e depois T8, enquanto as próximas iterações de 6:4 e 8:6 aconteceriam sempre sobre a mesma transposição de 4-24. Isso faz com o que o conteúdo completo de 10:4 envolva mais duas transposições de cada um dos tricordes.
Isso nos leva a outra forma de relacionar as interferências: o módulo delas. Por módulo quero dizer qual o intervalo no qual a escala se repete. É curioso, mas retornamos a noção de ciclo: o módulo reinscreve as interferências em ciclos intervalares. O ciclo 11:5, por exemplo, repete-se a cada semitom, ou seja, o padrão intervalar dele existe em um ciclo c7 e é como se a interferência contivesse, naturalmente, outro ciclo. Por outro lado, é como se, para a interferência se completar, ela precisasse passar por esse ciclo inteiro – o que liga ela a outras transposições dela, como modulações óbvias ou a extende por um espaço maior. Também é como se pudéssemos conectar interferências diferentes por módulo.
| Interferências por módulo | |||||||||
| Módulo | Interferências | ||||||||
| 0 | 4:3 | 6:4 | 8:3 | 8:6 | 9:4 | 9:8 | |||
| 2 | 7:2 | 11:10 | |||||||
| 3 | 5:3 | 9:7 | 11:9 | ||||||
| 4 | 7:4 | 8:5 | 10:8 | 11:8 | |||||
| 5 | 11:7 | ||||||||
| 6 | 3:2 | 6:5 | 7:6 | 9:2 | 9:6 | 10:3 | 10:6 | 10:9 | 11:6 |
| 7 | 11:5 | ||||||||
| 8 | 5:4 | 8:7 | 10:4 | 11:4 | |||||
| 9 | 7:3 | 9:5 | 11:3 | ||||||
| 10 | 5:2 | 10:7 | 11:2 | ||||||
| 11 | 7:5 | ||||||||
Um caso simples: as interferências 3:2 e 6:5 repetem em módulo 6 (ainda que 6:5 repita-se a 6 semitons duas oitavas acima) não compartilham uma classe resultante ou qualquer acorde, mas é como se elas compartilhassem um quadro comum. Não é uma relação forte, e seria preciso algum esforço pra torná-la audível, mas é uma relação a considerar quando estiver buscando relacionar, de maneira menos óbvia, duas interferências. Na tabela abaixo, agrupei por módulo as classes resultantes das interferências.

Provocações e Conclusões
O que fazer com tudo isso? Compor ou improvisar. O que isso tudo nos mostra é uma série de relações entre classes de conjunto, ciclos e interferências: escolha uma interferência, uma classe, um ciclo, um módulo e encontre suas relações. Tente fazê-las audíveis – ou não. Use-as como formas de gerar contraste ou de expandir uma ideia.
Ciclos geram interferências. Interferências contém tricordes, geram classes resultantes, possuem módulos. Tricordes conectam interferências.
Comecemos com 4:3: ela contém três conjuntos 3-2, 3-3 e 3-6; resulta em 6-Z28 e é módulo 0 (não é uma interferência transpositora). Através dos tricordes, 4:3 pivota para outras interferências (5:3, 7:3, 5:4, etc). Através de Mod 0, encaixa-se e aninha-se com outras em um mesmo ciclo (c12). Através de 6-Z28, compartilha notas com outras interferências. O caótico mapa abaixo descreve estas relações.
É interessante notar a predominância de potências distributivas dos componentes: 4 e 3 viram 2 e 6, 8 e 9. Mas também estranhezas como 5, 7, 11. Pode se tornar paralizante outra vez, mas a ideia é oferecer opções: comecemos com 4:3. O verso será escrito usando seu campo de possibilidades harmônicas. O refrão será escrito em 9:4 ou em 5:2. Quem sabe uma voz explore 11:2 enquanto o baixo segura 4:3. Ou simplesmente limitemos: começamos de 3-2, e decidimos realizar 3-2 em 4:3 para usar 3-3 e 3-6. Quem sabe a melodia seja em 6-Z28, enquanto a sequência de simultaneidades segue os limites de 4:3.
Para facilitar a exploração desta lógica, organizei em um PDF uma série de tabelas contendo todas as transposições de classes de interferências e as relações entre elas que discuti neste texto.